Fast Physical Activity Suggestions: Efficient Hyperparameter Learning in Mobile Health

Users can be supported to adopt healthy behaviors, such as regular physical activity, via relevant and timely suggestions on their mobile devices. Recently, reinforcement learning algorithms have been found to be effective for learning the optimal context under which to provide suggestions. However, these algorithms are not necessarily designed for the constraints posed by mobile health (mHealth) settings, that they be efficient, domain-informed and computationally affordable. We propose an algorithm for providing physical activity suggestions in mHealth settings. Using domain-science, we formulate a contextual bandit algorithm which makes use of a linear mixed effects model. We then introduce a procedure to efficiently perform hyper-parameter updating, using far less computational resources than competing approaches. Not only is our approach computationally efficient, it is also easily implemented with closed form matrix algebraic updates and we show improvements over state of the art approaches both in speed and accuracy of up to 99% and 56% respectively.

Streamlined Empirical Bayes Fitting of Linear Mixed Models in Mobile Health

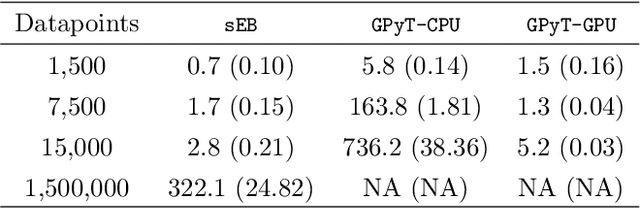
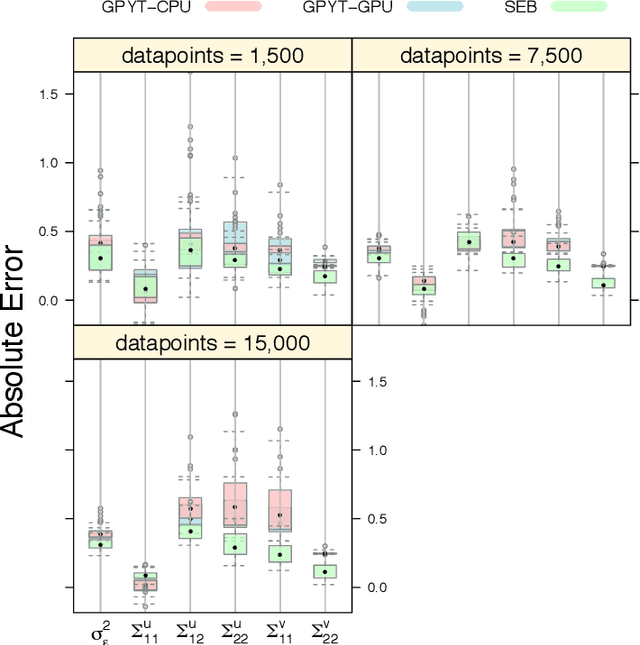
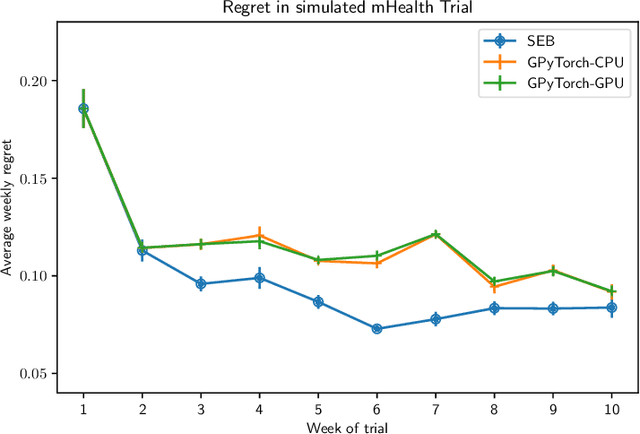
To effect behavior change a successful algorithm must make high-quality decisions in real-time. For example, a mobile health (mHealth) application designed to increase physical activity must make contextually relevant suggestions to motivate users. While machine learning offers solutions for certain stylized settings, such as when batch data can be processed offline, there is a dearth of approaches which can deliver high-quality solutions under the specific constraints of mHealth. We propose an algorithm which provides users with contextualized and personalized physical activity suggestions. This algorithm is able to overcome a challenge critical to mHealth that complex models be trained efficiently. We propose a tractable streamlined empirical Bayes procedure which fits linear mixed effects models in large-data settings. Our procedure takes advantage of sparsity introduced by hierarchical random effects to efficiently learn the posterior distribution of a linear mixed effects model. A key contribution of this work is that we provide explicit updates in order to learn both fixed effects, random effects and hyper-parameter values. We demonstrate the success of this approach in a mobile health (mHealth) reinforcement learning application, a domain in which fast computations are crucial for real time interventions. Not only is our approach computationally efficient, it is also easily implemented with closed form matrix algebraic updates and we show improvements over state of the art approaches both in speed and accuracy of up to 99% and 56% respectively.

Streamlined Variational Inference for Linear Mixed Models with Crossed Random Effects

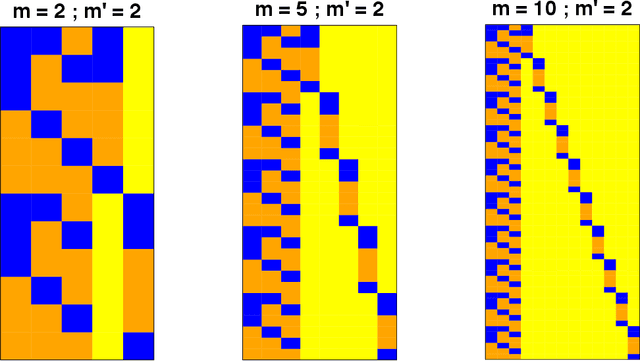
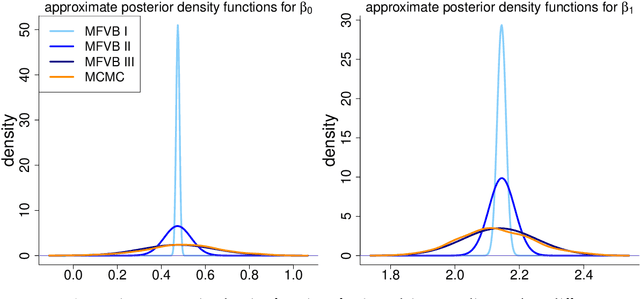
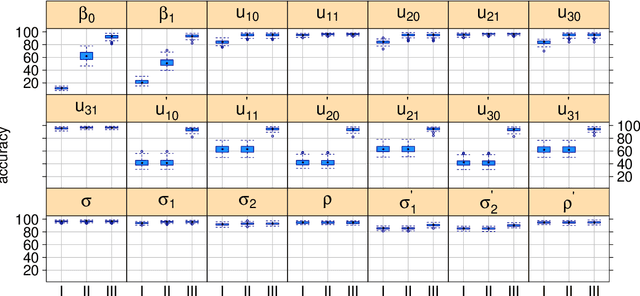
We derive streamlined mean field variational Bayes algorithms for fitting linear mixed models with crossed random effects. In the most general situation, where the dimensions of the crossed groups are arbitrarily large, streamlining is hindered by lack of sparseness in the underlying least squares system. Because of this fact we also consider a hierarchy of relaxations of the mean field product restriction. The least stringent product restriction delivers a high degree of inferential accuracy. However, this accuracy must be mitigated against its higher storage and computing demands. Faster sparse storage and computing alternatives are also provided, but come with the price of diminished inferential accuracy. This article provides full algorithmic details of three variational inference strategies, presents detailed empirical results on their pros and cons and, thus, guides the users on their choice of variational inference approach depending on the problem size and computing resources.