A Variational Inference Framework for Inverse Problems

We present a framework for fitting inverse problem models via variational Bayes approximations. This methodology guarantees flexibility to statistical model specification for a broad range of applications, good accuracy performances and reduced model fitting times, when compared with standard Markov chain Monte Carlo methods. The message passing and factor graph fragment approach to variational Bayes we describe facilitates streamlined implementation of approximate inference algorithms and forms the basis to software development. Such approach allows for supple inclusion of numerous response distributions and penalizations into the inverse problem model. Albeit our analysis is circumscribed to one- and two-dimensional response variables, we lay down an infrastructure where streamlining algorithmic steps based on nullifying weak interactions between variables are extendible to inverse problems in higher dimensions. Image processing applications motivated by biomedical and archaeological problems are included as illustrations.

Streamlined Variational Inference for Linear Mixed Models with Crossed Random Effects

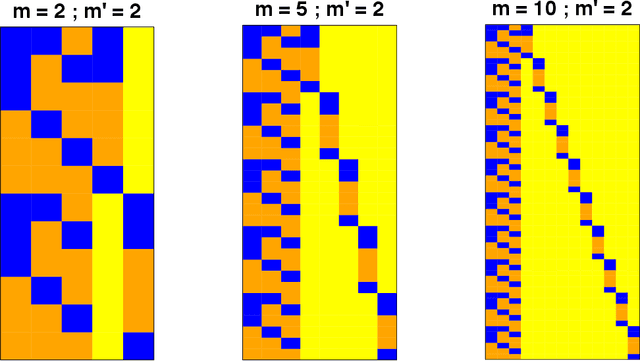
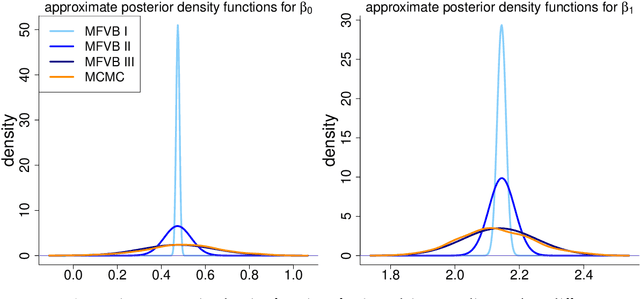
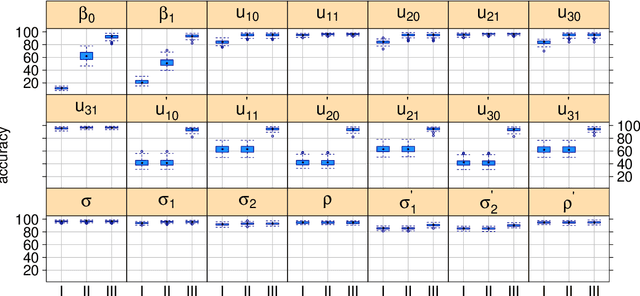
We derive streamlined mean field variational Bayes algorithms for fitting linear mixed models with crossed random effects. In the most general situation, where the dimensions of the crossed groups are arbitrarily large, streamlining is hindered by lack of sparseness in the underlying least squares system. Because of this fact we also consider a hierarchy of relaxations of the mean field product restriction. The least stringent product restriction delivers a high degree of inferential accuracy. However, this accuracy must be mitigated against its higher storage and computing demands. Faster sparse storage and computing alternatives are also provided, but come with the price of diminished inferential accuracy. This article provides full algorithmic details of three variational inference strategies, presents detailed empirical results on their pros and cons and, thus, guides the users on their choice of variational inference approach depending on the problem size and computing resources.