Streamlined Variational Inference for Linear Mixed Models with Crossed Random Effects
Paper and Code
Oct 04, 2019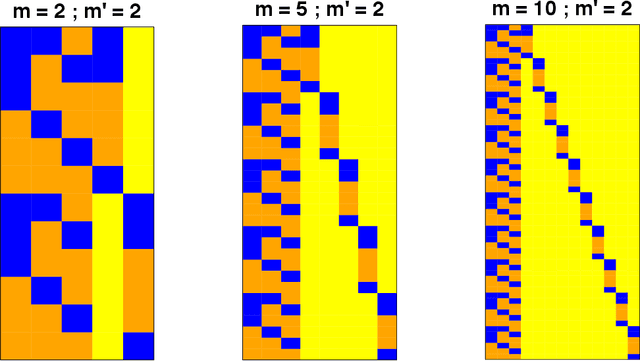

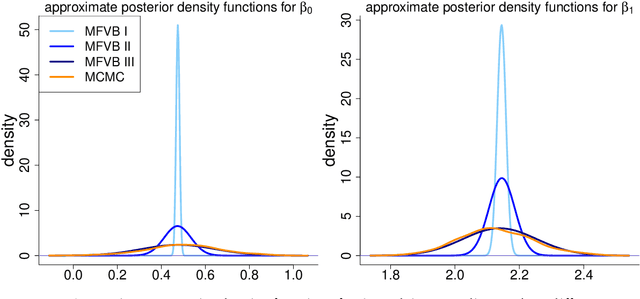
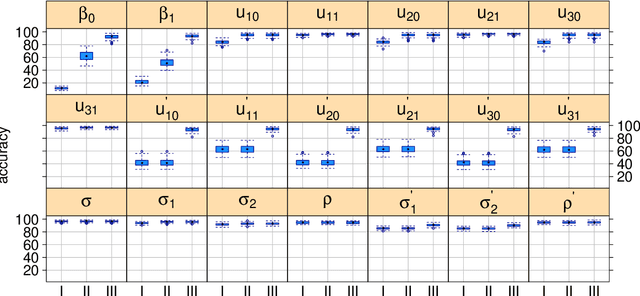
We derive streamlined mean field variational Bayes algorithms for fitting linear mixed models with crossed random effects. In the most general situation, where the dimensions of the crossed groups are arbitrarily large, streamlining is hindered by lack of sparseness in the underlying least squares system. Because of this fact we also consider a hierarchy of relaxations of the mean field product restriction. The least stringent product restriction delivers a high degree of inferential accuracy. However, this accuracy must be mitigated against its higher storage and computing demands. Faster sparse storage and computing alternatives are also provided, but come with the price of diminished inferential accuracy. This article provides full algorithmic details of three variational inference strategies, presents detailed empirical results on their pros and cons and, thus, guides the users on their choice of variational inference approach depending on the problem size and computing resources.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge