Multilingual Email Zoning

The segmentation of emails into functional zones (also dubbed email zoning) is a relevant preprocessing step for most NLP tasks that deal with emails. However, despite the multilingual character of emails and their applications, previous literature regarding email zoning corpora and systems was developed essentially for English. In this paper, we analyse the existing email zoning corpora and propose a new multilingual benchmark composed of 625 emails in Portuguese, Spanish and French. Moreover, we introduce OKAPI, the first multilingual email segmentation model based on a language agnostic sentence encoder. Besides generalizing well for unseen languages, our model is competitive with current English benchmarks, and reached new state-of-the-art performances for domain adaptation tasks in English.

Interleaved Sequence RNNs for Fraud Detection

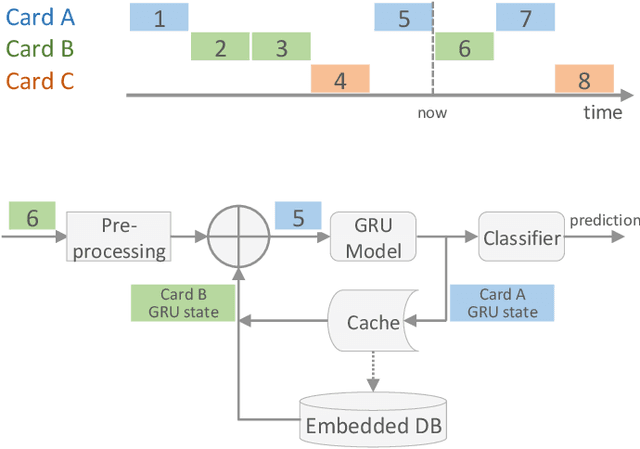
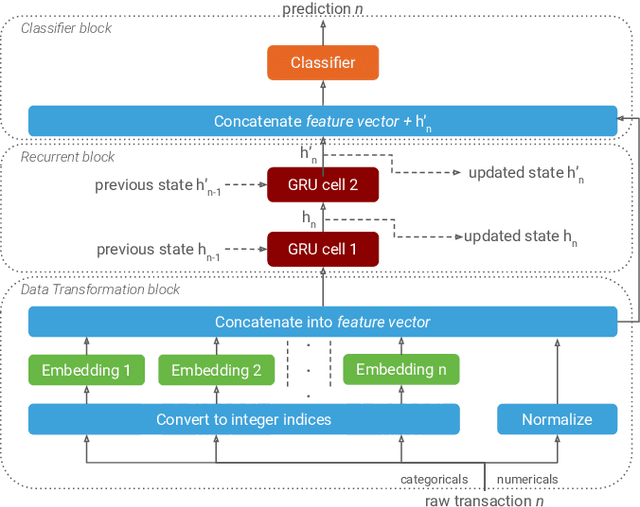
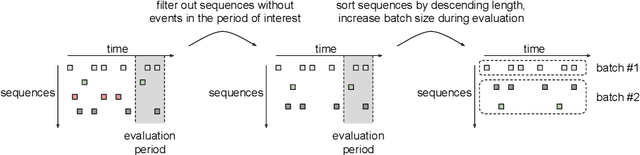
Payment card fraud causes multibillion dollar losses for banks and merchants worldwide, often fueling complex criminal activities. To address this, many real-time fraud detection systems use tree-based models, demanding complex feature engineering systems to efficiently enrich transactions with historical data while complying with millisecond-level latencies. In this work, we do not require those expensive features by using recurrent neural networks and treating payments as an interleaved sequence, where the history of each card is an unbounded, irregular sub-sequence. We present a complete RNN framework to detect fraud in real-time, proposing an efficient ML pipeline from preprocessing to deployment. We show that these feature-free, multi-sequence RNNs outperform state-of-the-art models saving millions of dollars in fraud detection and using fewer computational resources.

Deconvolving Images with Unknown Boundaries Using the Alternating Direction Method of Multipliers

The alternating direction method of multipliers (ADMM) has recently sparked interest as a flexible and efficient optimization tool for imaging inverse problems, namely deconvolution and reconstruction under non-smooth convex regularization. ADMM achieves state-of-the-art speed by adopting a divide and conquer strategy, wherein a hard problem is split into simpler, efficiently solvable sub-problems (e.g., using fast Fourier or wavelet transforms, or simple proximity operators). In deconvolution, one of these sub-problems involves a matrix inversion (i.e., solving a linear system), which can be done efficiently (in the discrete Fourier domain) if the observation operator is circulant, i.e., under periodic boundary conditions. This paper extends ADMM-based image deconvolution to the more realistic scenario of unknown boundary, where the observation operator is modeled as the composition of a convolution (with arbitrary boundary conditions) with a spatial mask that keeps only pixels that do not depend on the unknown boundary. The proposed approach also handles, at no extra cost, problems that combine the recovery of missing pixels (i.e., inpainting) with deconvolution. We show that the resulting algorithms inherit the convergence guarantees of ADMM and illustrate its performance on non-periodic deblurring (with and without inpainting of interior pixels) under total-variation and frame-based regularization.