Community detection in complex networks via node similarity, graph representation learning, and hierarchical clustering

Community detection is a critical challenge in the analysis of real-world graphs and complex networks, including social, transportation, citation, cybersecurity networks, and food webs. Motivated by many similarities between community detection and clustering in Euclidean spaces, we propose three algorithm frameworks to apply hierarchical clustering methods for community detection in graphs. We show that using our methods, it is possible to apply various linkage-based (single-, complete-, average- linkage, Ward, Genie) clustering algorithms to find communities based on vertex similarity matrices, eigenvector matrices thereof, and Euclidean vector representations of nodes. We convey a comprehensive analysis of choices for each framework, including state-of-the-art graph representation learning algorithms, such as Deep Neural Graph Representation, and a vertex proximity matrix known to yield high-quality results in machine learning -- Positive Pointwise Mutual Information. Overall, we test over a hundred combinations of framework components and show that some -- including Wasserman-Faust and PPMI proximity, DNGR representation -- can compete with algorithms such as state-of-the-art Leiden and Louvain and easily outperform other known community detection algorithms. Notably, our algorithms remain hierarchical and allow the user to specify any number of clusters a priori.

Hierarchical Clustering with OWA-based Linkages, the Lance-Williams Formula, and Dendrogram Inversions

Agglomerative hierarchical clustering based on Ordered Weighted Averaging (OWA) operators not only generalises the single, complete, and average linkages, but also includes intercluster distances based on a few nearest or farthest neighbours, trimmed and winsorised means of pairwise point similarities, amongst many others. We explore the relationships between the famous Lance-Williams update formula and the extended OWA-based linkages with weights generated via infinite coefficient sequences. Furthermore, we provide some conditions for the weight generators to guarantee the resulting dendrograms to be free from unaesthetic inversions.

Clustering with minimum spanning trees: How good can it be?

Minimum spanning trees (MSTs) provide a convenient representation of datasets in numerous pattern recognition activities. Moreover, they are relatively fast to compute. In this paper, we quantify the extent to which they can be meaningful in data clustering tasks. By identifying the upper bounds for the agreement between the best (oracle) algorithm and the expert labels from a large battery of benchmark data, we discover that MST methods can overall be very competitive. Next, instead of proposing yet another algorithm that performs well on a limited set of examples, we review, study, extend, and generalise existing, the state-of-the-art MST-based partitioning schemes, which leads to a few new and interesting approaches. It turns out that the Genie method and the information-theoretic approaches often outperform the non-MST algorithms such as k-means, Gaussian mixtures, spectral clustering, BIRCH, and classical hierarchical agglomerative procedures.

Deep R Programming

Deep R Programming is a comprehensive course on one of the most popular languages in data science (statistical computing, graphics, machine learning, data wrangling and analytics). It introduces the base language in-depth and is aimed at ambitious students, practitioners, and researchers who would like to become independent users of this powerful environment. This textbook is a non-profit project. Its online and PDF versions are freely available at <https://deepr.gagolewski.com/>. This early draft is distributed in the hope that it will be useful.

Minimalist Data Wrangling with Python

Minimalist Data Wrangling with Python is envisaged as a student's first introduction to data science, providing a high-level overview as well as discussing key concepts in detail. We explore methods for cleaning data gathered from different sources, transforming, selecting, and extracting features, performing exploratory data analysis and dimensionality reduction, identifying naturally occurring data clusters, modelling patterns in data, comparing data between groups, and reporting the results. This textbook is a non-profit project. Its online and PDF versions are freely available at https://datawranglingpy.gagolewski.com/.

A Framework for Benchmarking Clustering Algorithms

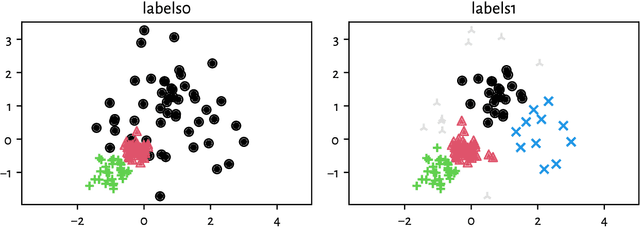
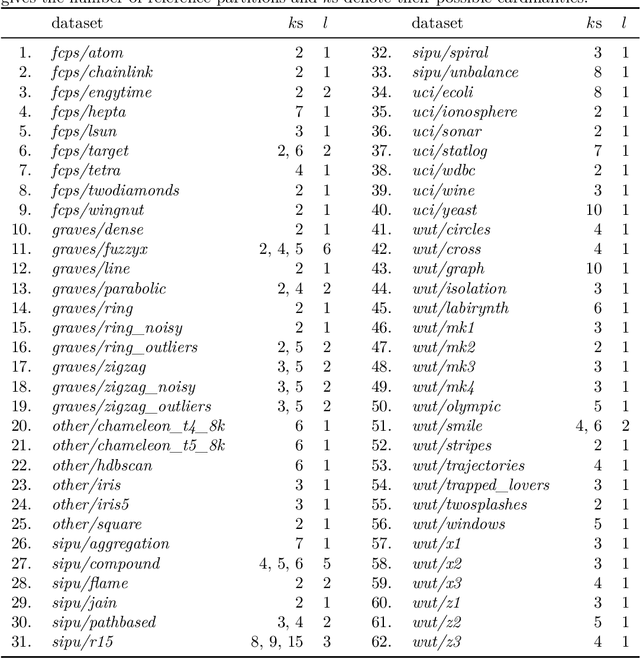
The evaluation of clustering algorithms can be performed by running them on a variety of benchmark problems, and comparing their outputs to the reference, ground-truth groupings provided by experts. Unfortunately, many research papers and graduate theses consider only a small number of datasets. Also, rarely the fact that there can be many equally valid ways to cluster a given problem set is taken into account. In order to overcome these limitations, we have developed a framework whose aim is to introduce a consistent methodology for testing clustering algorithms. Furthermore, we have aggregated, polished, and standardised many clustering benchmark batteries referred to across the machine learning and data mining literature, and included new datasets of different dimensionalities, sizes, and cluster types. An interactive datasets explorer, the documentation of the Python API, a description of the ways to interact with the framework from other programming languages such as R or MATLAB, and other details are all provided at https://clustering-benchmarks.gagolewski.com.

Genie: A new, fast, and outlier-resistant hierarchical clustering algorithm

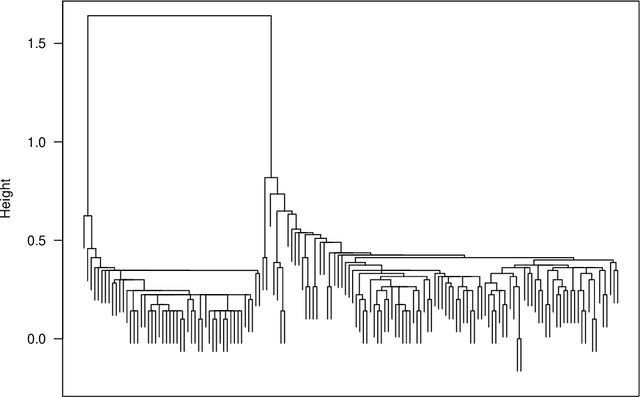
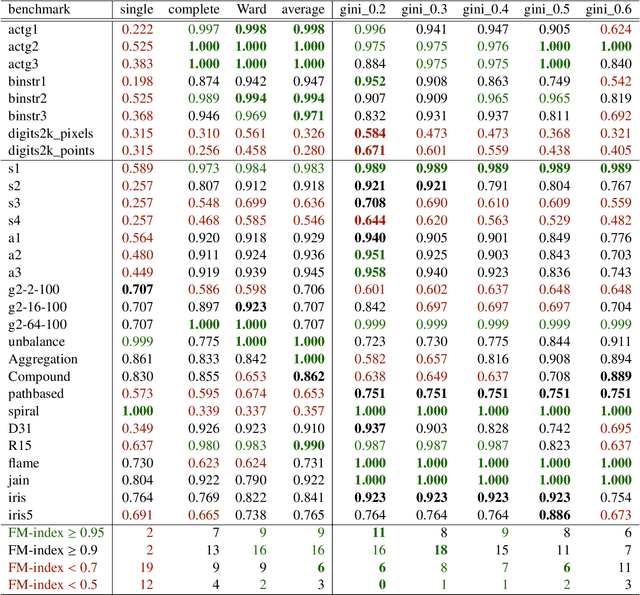
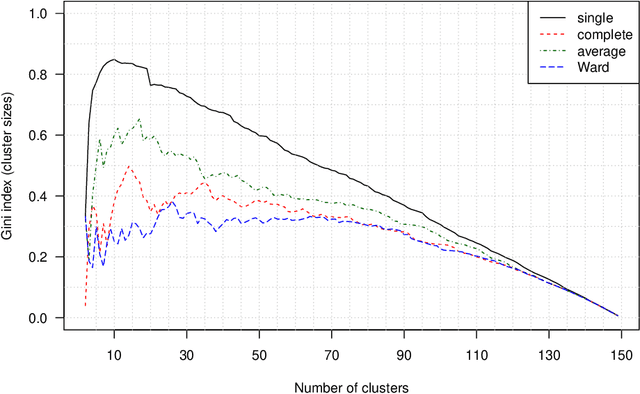
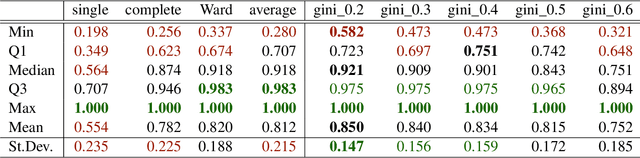
The time needed to apply a hierarchical clustering algorithm is most often dominated by the number of computations of a pairwise dissimilarity measure. Such a constraint, for larger data sets, puts at a disadvantage the use of all the classical linkage criteria but the single linkage one. However, it is known that the single linkage clustering algorithm is very sensitive to outliers, produces highly skewed dendrograms, and therefore usually does not reflect the true underlying data structure -- unless the clusters are well-separated. To overcome its limitations, we propose a new hierarchical clustering linkage criterion called Genie. Namely, our algorithm links two clusters in such a way that a chosen economic inequity measure (e.g., the Gini- or Bonferroni-index) of the cluster sizes does not drastically increase above a given threshold. The presented benchmarks indicate a high practical usefulness of the introduced method: it most often outperforms the Ward or average linkage in terms of the clustering quality while retaining the single linkage's speed. The Genie algorithm is easily parallelizable and thus may be run on multiple threads to speed up its execution even further. Its memory overhead is small: there is no need to precompute the complete distance matrix to perform the computations in order to obtain a desired clustering. It can be applied on arbitrary spaces equipped with a dissimilarity measure, e.g., on real vectors, DNA or protein sequences, images, rankings, informetric data, etc. A reference implementation of the algorithm has been included in the open source 'genie' package for R. See also https://genieclust.gagolewski.com for a new implementation (genieclust) -- available for both R and Python.

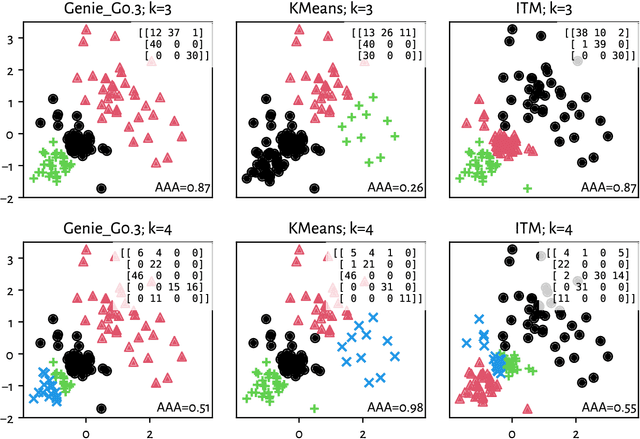
Adjusted Asymmetric Accuracy: A Well-Behaving External Cluster Validity Measure

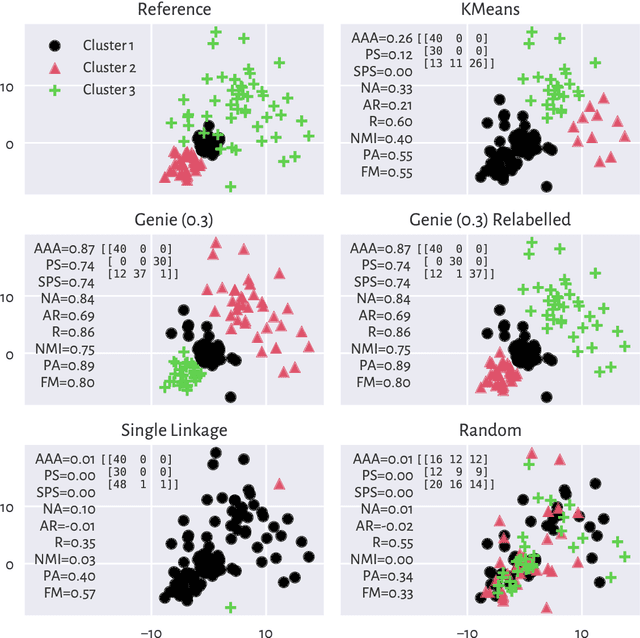
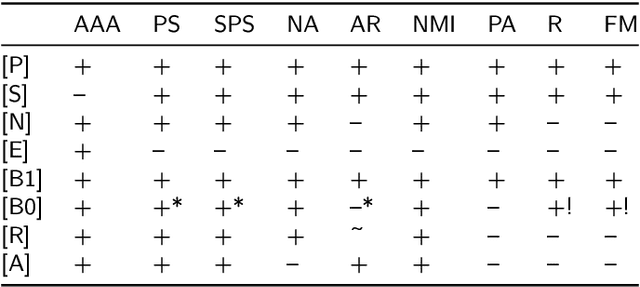
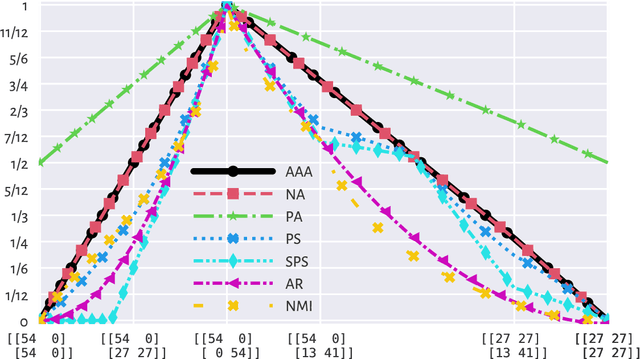
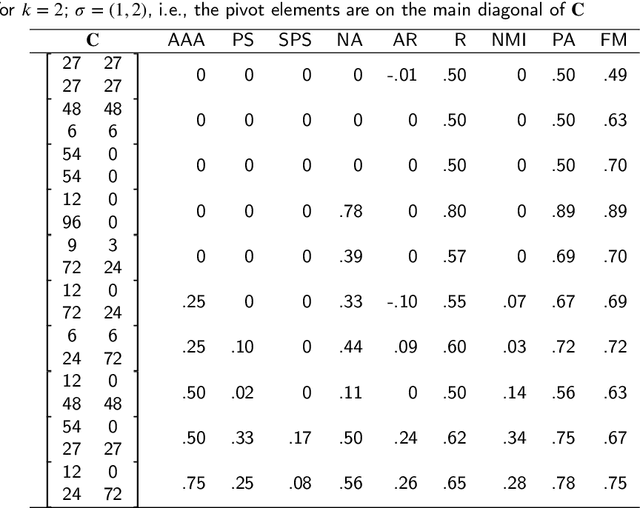
There is no, nor will there ever be, single best clustering algorithm, but we would still like to be able to pinpoint those which are well-performing on certain task types and filter out the systematically disappointing ones. Clustering algorithms are traditionally evaluated using either internal or external validity measures. Internal measures quantify different aspects of the obtained partitions, e.g., the average degree of cluster compactness or point separability. Yet, their validity is questionable because the clusterings they promote can sometimes be meaningless. External measures, on the other hand, compare the algorithms' outputs to the reference, ground truth groupings that are provided by experts. The commonly-used classical partition similarity scores, such as the normalised mutual information, Fowlkes-Mallows, or adjusted Rand index, might not possess all the desirable properties, e.g., they do not identify pathological edge cases correctly. Furthermore, they are not nicely interpretable: it is hard to say what a score of 0.8 really means. Its behaviour might also vary as the number of true clusters changes. This makes comparing clustering algorithms across many benchmark datasets difficult. To remedy this, we propose and analyse a new measure: an asymmetric version of the optimal set-matching accuracy. It is corrected for chance and the imbalancedness of cluster sizes.

Are Cluster Validity Measures (In)valid?

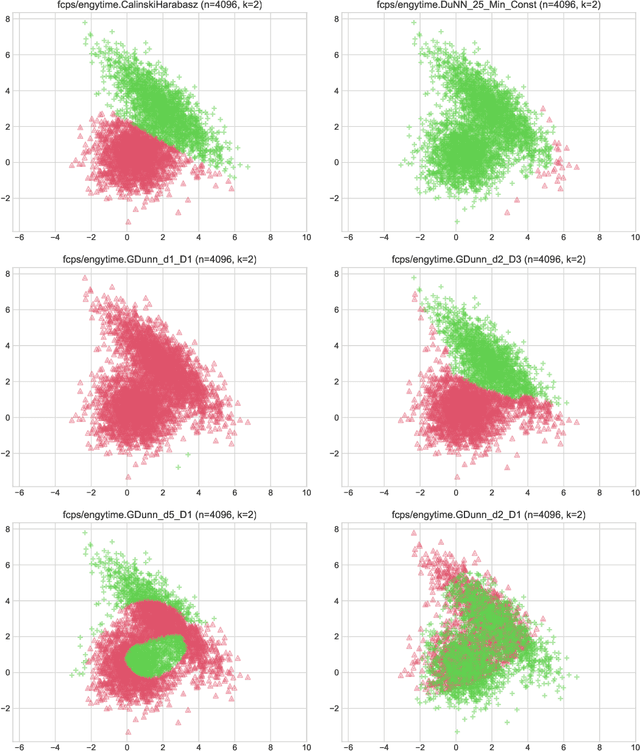
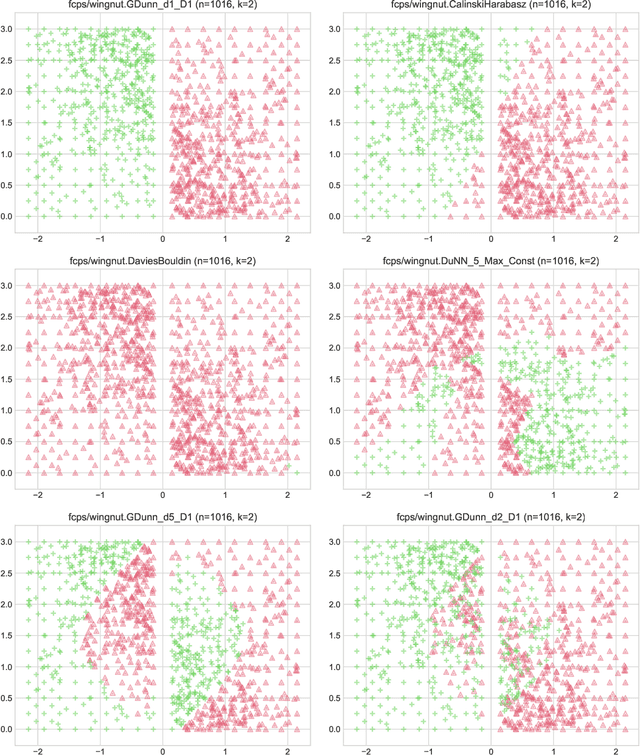
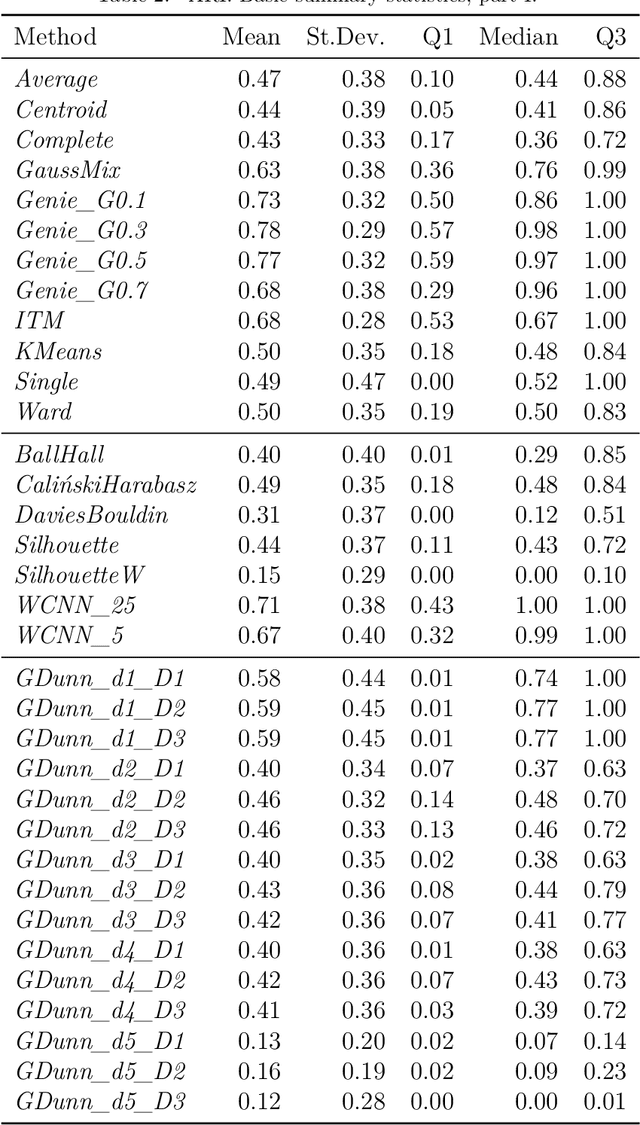
Internal cluster validity measures (such as the Calinski-Harabasz, Dunn, or Davies-Bouldin indices) are frequently used for selecting the appropriate number of partitions a dataset should be split into. In this paper we consider what happens if we treat such indices as objective functions in unsupervised learning activities. Is the optimal grouping with regards to, say, the Silhouette index really meaningful? It turns out that many cluster (in)validity indices promote clusterings that match expert knowledge quite poorly. We also introduce a new, well-performing variant of the Dunn index that is built upon OWA operators and the near-neighbour graph so that subspaces of higher density, regardless of their shapes, can be separated from each other better.