Hierarchical Clustering with OWA-based Linkages, the Lance-Williams Formula, and Dendrogram Inversions

Agglomerative hierarchical clustering based on Ordered Weighted Averaging (OWA) operators not only generalises the single, complete, and average linkages, but also includes intercluster distances based on a few nearest or farthest neighbours, trimmed and winsorised means of pairwise point similarities, amongst many others. We explore the relationships between the famous Lance-Williams update formula and the extended OWA-based linkages with weights generated via infinite coefficient sequences. Furthermore, we provide some conditions for the weight generators to guarantee the resulting dendrograms to be free from unaesthetic inversions.

Clustering with minimum spanning trees: How good can it be?

Minimum spanning trees (MSTs) provide a convenient representation of datasets in numerous pattern recognition activities. Moreover, they are relatively fast to compute. In this paper, we quantify the extent to which they can be meaningful in data clustering tasks. By identifying the upper bounds for the agreement between the best (oracle) algorithm and the expert labels from a large battery of benchmark data, we discover that MST methods can overall be very competitive. Next, instead of proposing yet another algorithm that performs well on a limited set of examples, we review, study, extend, and generalise existing, the state-of-the-art MST-based partitioning schemes, which leads to a few new and interesting approaches. It turns out that the Genie method and the information-theoretic approaches often outperform the non-MST algorithms such as k-means, Gaussian mixtures, spectral clustering, BIRCH, and classical hierarchical agglomerative procedures.

Genie: A new, fast, and outlier-resistant hierarchical clustering algorithm

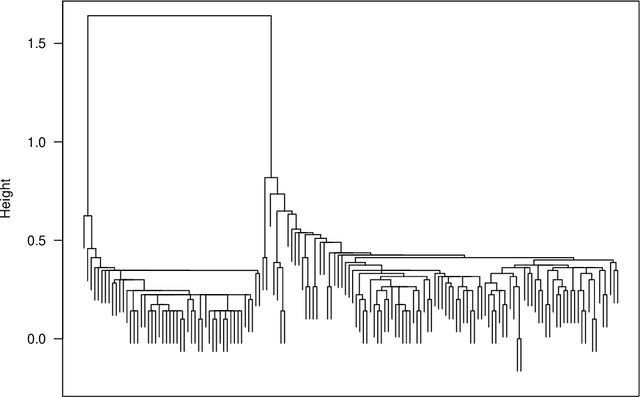
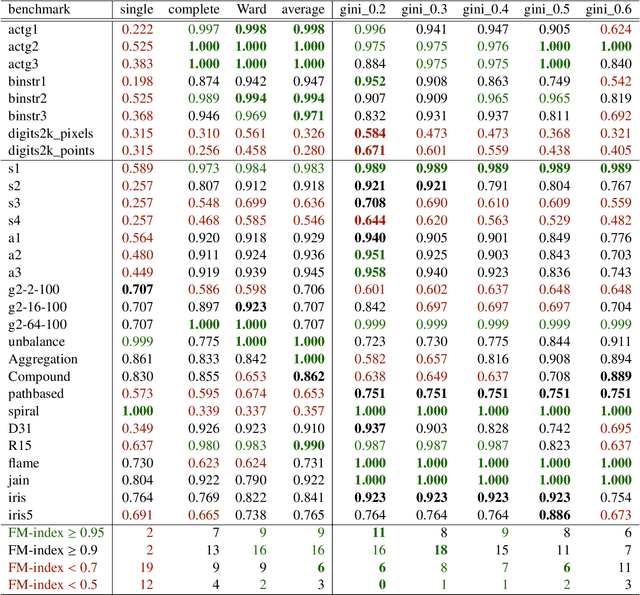
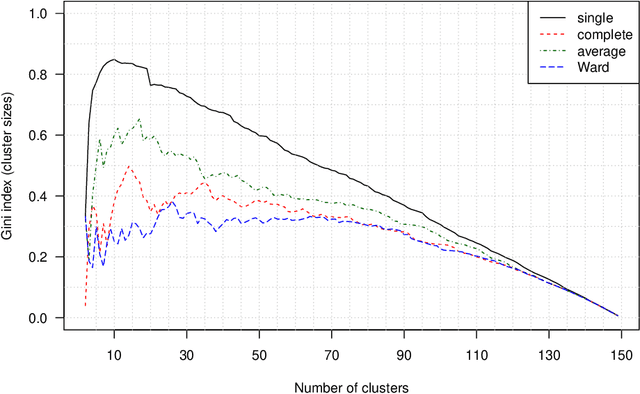
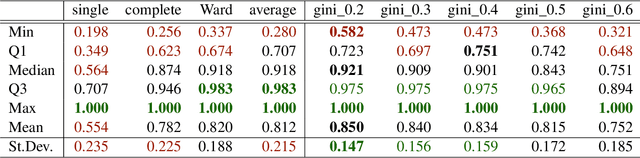
The time needed to apply a hierarchical clustering algorithm is most often dominated by the number of computations of a pairwise dissimilarity measure. Such a constraint, for larger data sets, puts at a disadvantage the use of all the classical linkage criteria but the single linkage one. However, it is known that the single linkage clustering algorithm is very sensitive to outliers, produces highly skewed dendrograms, and therefore usually does not reflect the true underlying data structure -- unless the clusters are well-separated. To overcome its limitations, we propose a new hierarchical clustering linkage criterion called Genie. Namely, our algorithm links two clusters in such a way that a chosen economic inequity measure (e.g., the Gini- or Bonferroni-index) of the cluster sizes does not drastically increase above a given threshold. The presented benchmarks indicate a high practical usefulness of the introduced method: it most often outperforms the Ward or average linkage in terms of the clustering quality while retaining the single linkage's speed. The Genie algorithm is easily parallelizable and thus may be run on multiple threads to speed up its execution even further. Its memory overhead is small: there is no need to precompute the complete distance matrix to perform the computations in order to obtain a desired clustering. It can be applied on arbitrary spaces equipped with a dissimilarity measure, e.g., on real vectors, DNA or protein sequences, images, rankings, informetric data, etc. A reference implementation of the algorithm has been included in the open source 'genie' package for R. See also https://genieclust.gagolewski.com for a new implementation (genieclust) -- available for both R and Python.

Are Cluster Validity Measures (In)valid?

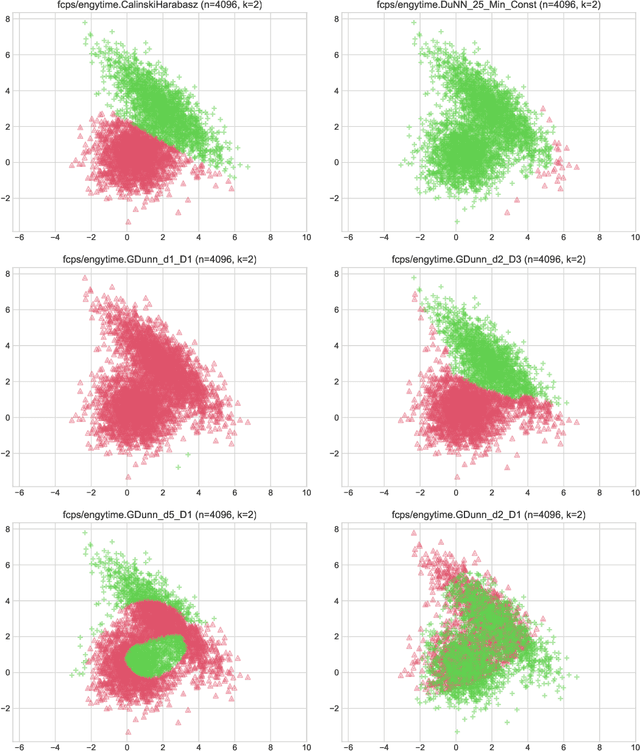
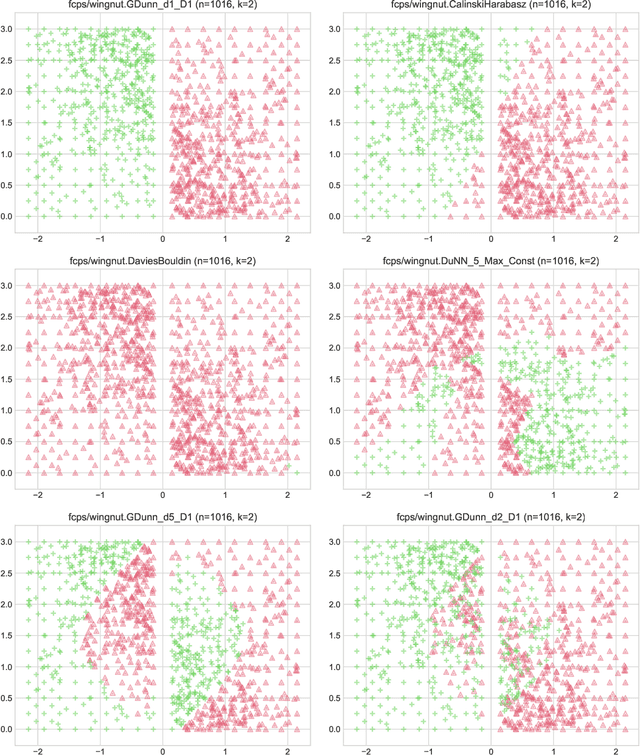
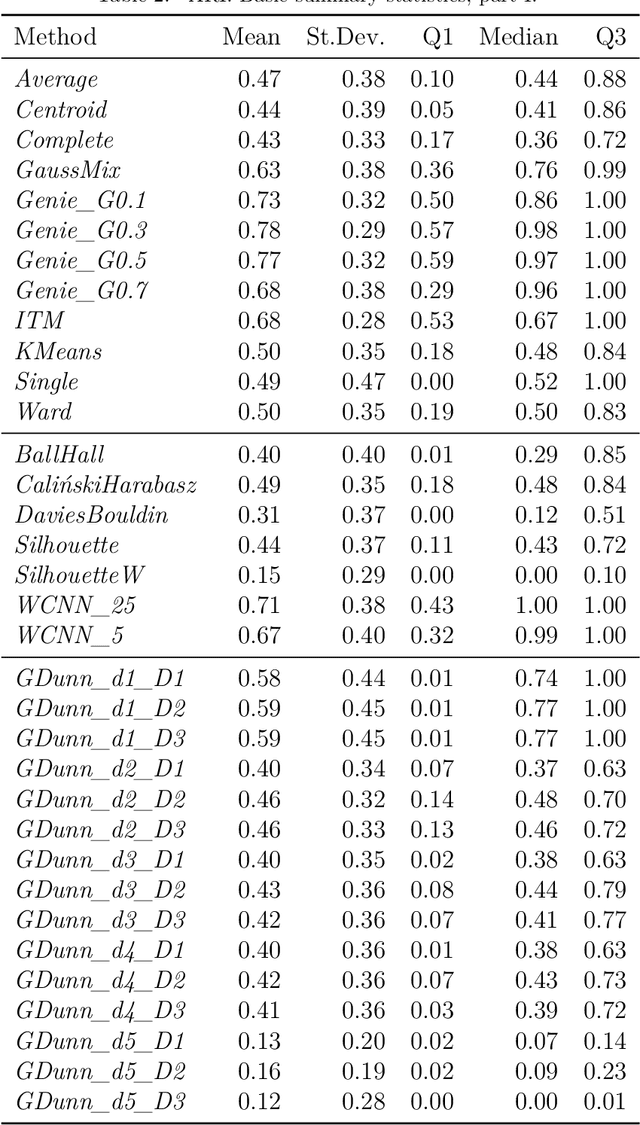
Internal cluster validity measures (such as the Calinski-Harabasz, Dunn, or Davies-Bouldin indices) are frequently used for selecting the appropriate number of partitions a dataset should be split into. In this paper we consider what happens if we treat such indices as objective functions in unsupervised learning activities. Is the optimal grouping with regards to, say, the Silhouette index really meaningful? It turns out that many cluster (in)validity indices promote clusterings that match expert knowledge quite poorly. We also introduce a new, well-performing variant of the Dunn index that is built upon OWA operators and the near-neighbour graph so that subspaces of higher density, regardless of their shapes, can be separated from each other better.