Double framed moduli spaces of quiver representations

Motivated by problems in the neural networks setting, we study moduli spaces of double framed quiver representations and give both a linear algebra description and a representation theoretic description of these moduli spaces. We define a network category whose isomorphism classes of objects correspond to the orbits of quiver representations, in which neural networks map input data. We then prove that the output of a neural network depends only on the corresponding point in the moduli space. Finally, we present a different perspective on mapping neural networks with a specific activation function, called ReLU, to a moduli space using the symplectic reduction approach to quiver moduli.

Neural Teleportation

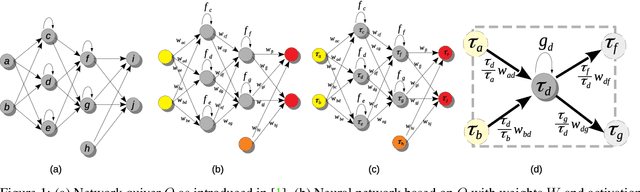
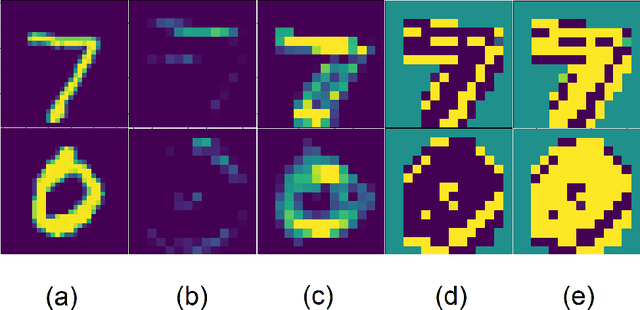
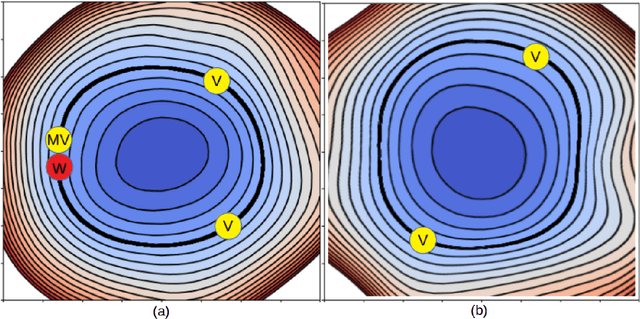
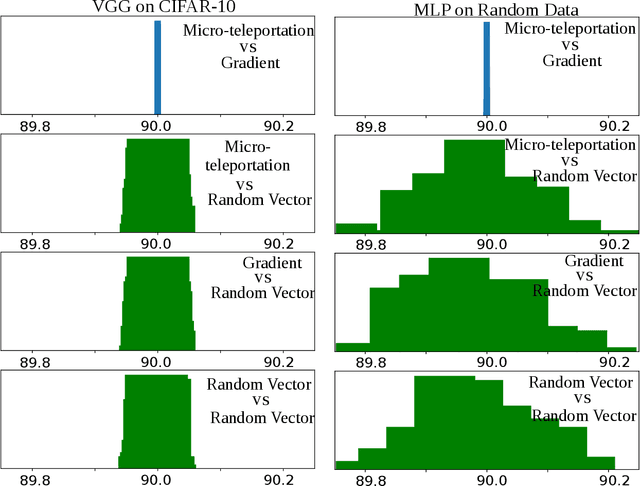
In this paper, we explore a process called neural teleportation, a mathematical consequence of applying quiver representation theory to neural networks. Neural teleportation "teleports" a network to a new position in the weight space, while leaving its function unchanged. This concept generalizes the notion of positive scale invariance of ReLU networks to any network with any activation functions and any architecture. In this paper, we shed light on surprising and counter-intuitive consequences neural teleportation has on the loss landscape. In particular, we show that teleportation can be used to explore loss level curves, that it changes the loss landscape, sharpens global minima and boosts back-propagated gradients. From these observations, we demonstrate that teleportation accelerates training when used during initialization regardless of the model, its activation function, the loss function, and the training data. Our results can be reproduced with the code available here: https://github.com/vitalab/neuralteleportation.