Marcin B. Tomczak
Compatible features for Monotonic Policy Improvement
Oct 30, 2019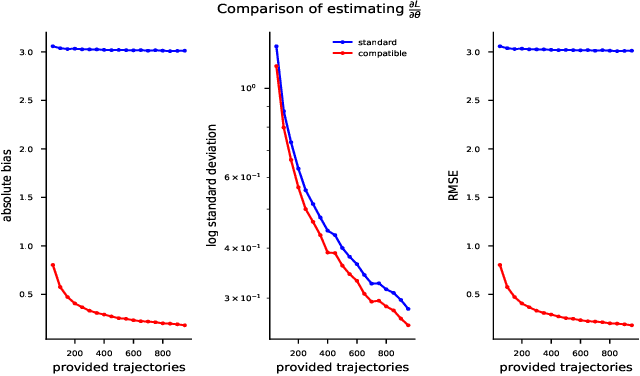
Abstract:Recent policy optimization approaches have achieved substantial empirical success by constructing surrogate optimization objectives. The Approximate Policy Iteration objective (Schulman et al., 2015a; Kakade and Langford, 2002) has become a standard optimization target for reinforcement learning problems. Using this objective in practice requires an estimator of the advantage function. Policy optimization methods such as those proposed in Schulman et al. (2015b) estimate the advantages using a parametric critic. In this work we establish conditions under which the parametric approximation of the critic does not introduce bias to the updates of surrogate objective. These results hold for a general class of parametric policies, including deep neural networks. We obtain a result analogous to the compatible features derived for the original Policy Gradient Theorem (Sutton et al., 1999). As a result, we also identify a previously unknown bias that current state-of-the-art policy optimization algorithms (Schulman et al., 2015a, 2017) have introduced by not employing these compatible features.
Policy Optimization Through Approximated Importance Sampling
Oct 09, 2019
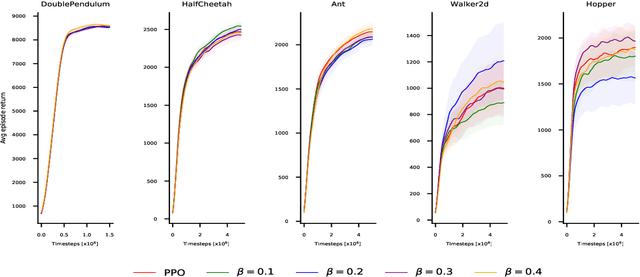
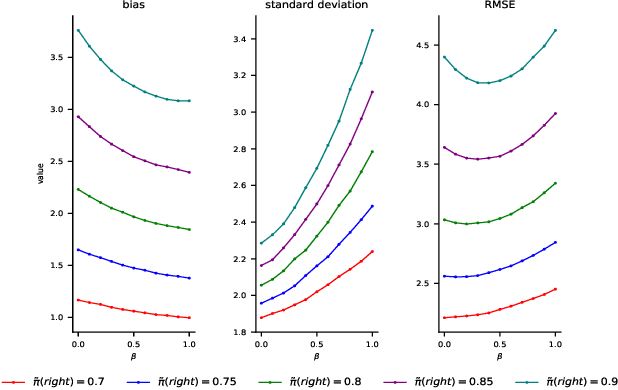
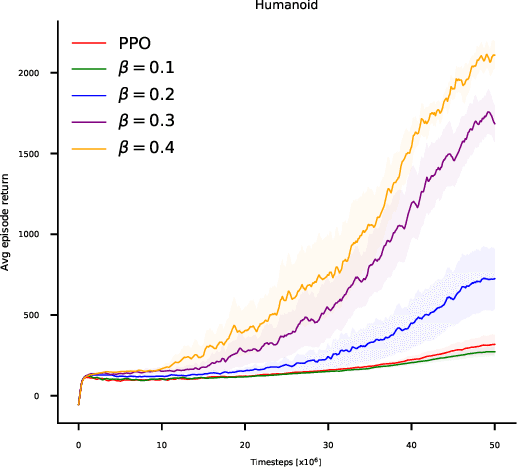
Abstract:Recent policy optimization approaches (Schulman et al., 2015a, 2017) have achieved substantial empirical successes by constructing new proxy optimization objectives. These proxy objectives allow stable and low variance policy learning, but require small policy updates to ensure that the proxy objective remains an accurate approximation of the target policy value. In this paper we derive an alternative objective that obtains the value of the target policy by applying importance sampling. This objective can be directly estimated from samples, as it takes an expectation over trajectories generated by the current policy. However, the basic importance sampled objective is not suitable for policy optimization, as it incurs unacceptable variance. We therefore introduce an approximation that allows us to directly trade-off the bias of approximation with the variance in policy updates. We show that our approximation unifies the proxy optimization approaches with the importance sampling objective and allows us to interpolate between them. We then provide a theoretical analysis of the method that directly quantifies the error term due to the approximation. Finally, we obtain a practical algorithm by optimizing the introduced objective with proximal policy optimization techniques (Schulman etal., 2017). We empirically demonstrate that the result-ing algorithm yields superior performance on continuous control benchmarks
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge