More Recent Advances in (Hyper)Graph Partitioning

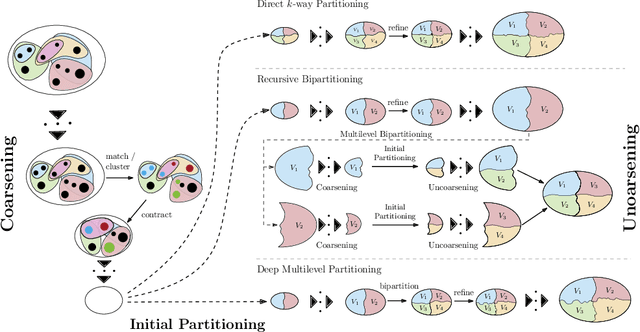
In recent years, significant advances have been made in the design and evaluation of balanced (hyper)graph partitioning algorithms. We survey trends of the last decade in practical algorithms for balanced (hyper)graph partitioning together with future research directions. Our work serves as an update to a previous survey on the topic. In particular, the survey extends the previous survey by also covering hypergraph partitioning and streaming algorithms, and has an additional focus on parallel algorithms.

Local Motif Clustering via (Hyper)Graph Partitioning

A widely-used operation on graphs is local clustering, i.e., extracting a well-characterized community around a seed node without the need to process the whole graph. Recently local motif clustering has been proposed: it looks for a local cluster based on the distribution of motifs. Since this local clustering perspective is relatively new, most approaches proposed for it are extensions of statistical and numerical methods previously used for edge-based local clustering, while the available combinatorial approaches are still few and relatively simple. In this work, we build a hypergraph and a graph model which both represent the motif-distribution around the seed node. We solve these models using sophisticated combinatorial algorithms designed for (hyper)graph partitioning. In extensive experiments with the triangle motif, we observe that our algorithm computes communities with a motif conductance value being one third on average in comparison against the communities computed by the state-of-the-art tool MAPPR while being 6.3 times faster on average.