Unleashing Graph Partitioning for Large-Scale Nearest Neighbor Search

We consider the fundamental problem of decomposing a large-scale approximate nearest neighbor search (ANNS) problem into smaller sub-problems. The goal is to partition the input points into neighborhood-preserving shards, so that the nearest neighbors of any point are contained in only a few shards. When a query arrives, a routing algorithm is used to identify the shards which should be searched for its nearest neighbors. This approach forms the backbone of distributed ANNS, where the dataset is so large that it must be split across multiple machines. In this paper, we design simple and highly efficient routing methods, and prove strong theoretical guarantees on their performance. A crucial characteristic of our routing algorithms is that they are inherently modular, and can be used with any partitioning method. This addresses a key drawback of prior approaches, where the routing algorithms are inextricably linked to their associated partitioning method. In particular, our new routing methods enable the use of balanced graph partitioning, which is a high-quality partitioning method without a naturally associated routing algorithm. Thus, we provide the first methods for routing using balanced graph partitioning that are extremely fast to train, admit low latency, and achieve high recall. We provide a comprehensive evaluation of our full partitioning and routing pipeline on billion-scale datasets, where it outperforms existing scalable partitioning methods by significant margins, achieving up to 2.14x higher QPS at 90% recall$@10$ than the best competitor.

More Recent Advances in (Hyper)Graph Partitioning

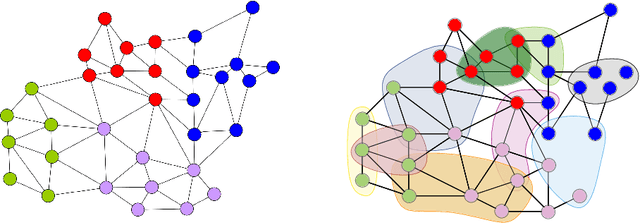
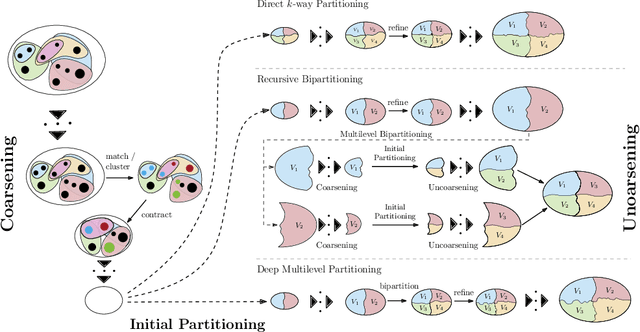
In recent years, significant advances have been made in the design and evaluation of balanced (hyper)graph partitioning algorithms. We survey trends of the last decade in practical algorithms for balanced (hyper)graph partitioning together with future research directions. Our work serves as an update to a previous survey on the topic. In particular, the survey extends the previous survey by also covering hypergraph partitioning and streaming algorithms, and has an additional focus on parallel algorithms.