On the Duality Between Retinex and Image Dehazing

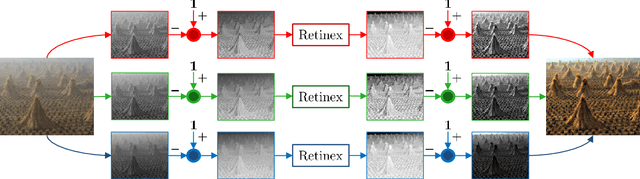
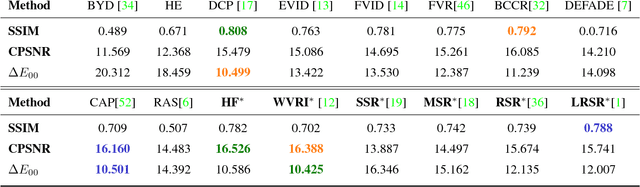
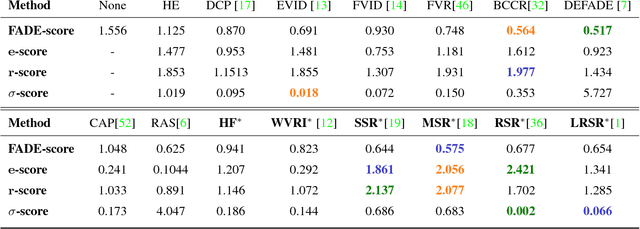
Image dehazing deals with the removal of undesired loss of visibility in outdoor images due to the presence of fog. Retinex is a color vision model mimicking the ability of the Human Visual System to robustly discount varying illuminations when observing a scene under different spectral lighting conditions. Retinex has been widely explored in the computer vision literature for image enhancement and other related tasks. While these two problems are apparently unrelated, the goal of this work is to show that they can be connected by a simple linear relationship. Specifically, most Retinex-based algorithms have the characteristic feature of always increasing image brightness, which turns them into ideal candidates for effective image dehazing by directly applying Retinex to a hazy image whose intensities have been inverted. In this paper, we give theoretical proof that Retinex on inverted intensities is a solution to the image dehazing problem. Comprehensive qualitative and quantitative results indicate that several classical and modern implementations of Retinex can be transformed into competing image dehazing algorithms performing on pair with more complex fog removal methods, and can overcome some of the main challenges associated with this problem.

A Contrario Selection of Optimal Partitions for Image Segmentation

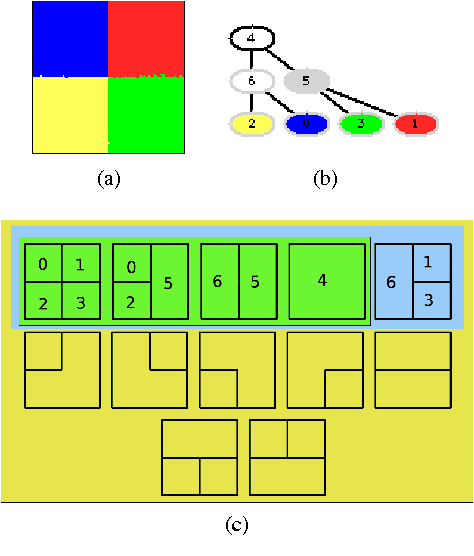
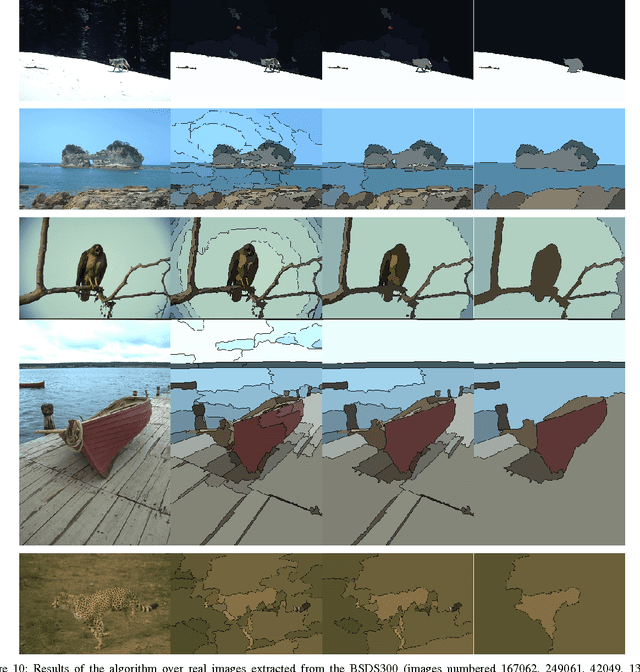
We present a novel segmentation algorithm based on a hierarchical representation of images. The main contribution of this work is to explore the capabilities of the A Contrario reasoning when applied to the segmentation problem, and to overcome the limitations of current algorithms within that framework. This exploratory approach has three main goals. Our first goal is to extend the search space of greedy merging algorithms to the set of all partitions spanned by a certain hierarchy, and to cast the segmentation as a selection problem within this space. In this way we increase the number of tested partitions and thus we potentially improve the segmentation results. In addition, this space is considerably smaller than the space of all possible partitions, thus we still keep the complexity controlled. Our second goal aims to improve the locality of region merging algorithms, which usually merge pairs of neighboring regions. In this work, we overcome this limitation by introducing a validation procedure for complete partitions, rather than for pairs of regions. The third goal is to perform an exhaustive experimental evaluation methodology in order to provide reproducible results. Finally, we embed the selection process on a statistical A Contrario framework which allows us to have only one free parameter related to the desired scale.