A Contrario Selection of Optimal Partitions for Image Segmentation
Paper and Code
May 06, 2013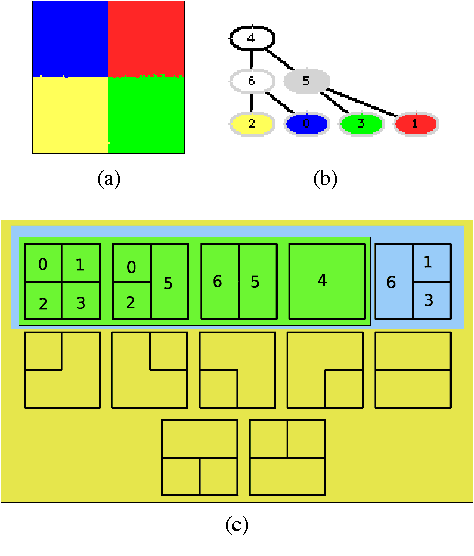
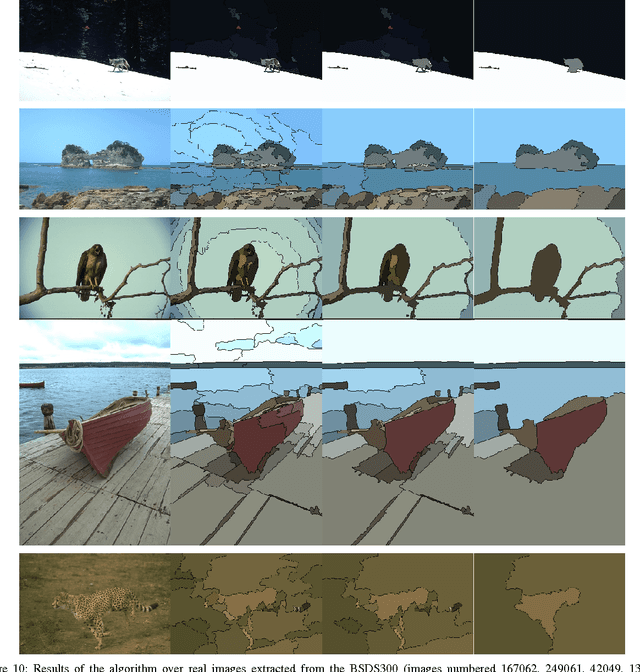


We present a novel segmentation algorithm based on a hierarchical representation of images. The main contribution of this work is to explore the capabilities of the A Contrario reasoning when applied to the segmentation problem, and to overcome the limitations of current algorithms within that framework. This exploratory approach has three main goals. Our first goal is to extend the search space of greedy merging algorithms to the set of all partitions spanned by a certain hierarchy, and to cast the segmentation as a selection problem within this space. In this way we increase the number of tested partitions and thus we potentially improve the segmentation results. In addition, this space is considerably smaller than the space of all possible partitions, thus we still keep the complexity controlled. Our second goal aims to improve the locality of region merging algorithms, which usually merge pairs of neighboring regions. In this work, we overcome this limitation by introducing a validation procedure for complete partitions, rather than for pairs of regions. The third goal is to perform an exhaustive experimental evaluation methodology in order to provide reproducible results. Finally, we embed the selection process on a statistical A Contrario framework which allows us to have only one free parameter related to the desired scale.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge