Equivalence of Additive and Multiplicative Coupling in Spiking Neural Networks

Spiking neural network models characterize the emergent collective dynamics of circuits of biological neurons and help engineer neuro-inspired solutions across fields. Most dynamical systems' models of spiking neural networks typically exhibit one of two major types of interactions: First, the response of a neuron's state variable to incoming pulse signals (spikes) may be additive and independent of its current state. Second, the response may depend on the current neuron's state and multiply a function of the state variable. Here we reveal that spiking neural network models with additive coupling are equivalent to models with multiplicative coupling for simultaneously modified intrinsic neuron time evolution. As a consequence, the same collective dynamics can be attained by state-dependent multiplicative and constant (state-independent) additive coupling. Such a mapping enables the transfer of theoretical insights between spiking neural network models with different types of interaction mechanisms as well as simpler and more effective engineering applications.

Stochastic facilitation in heteroclinic communication channels

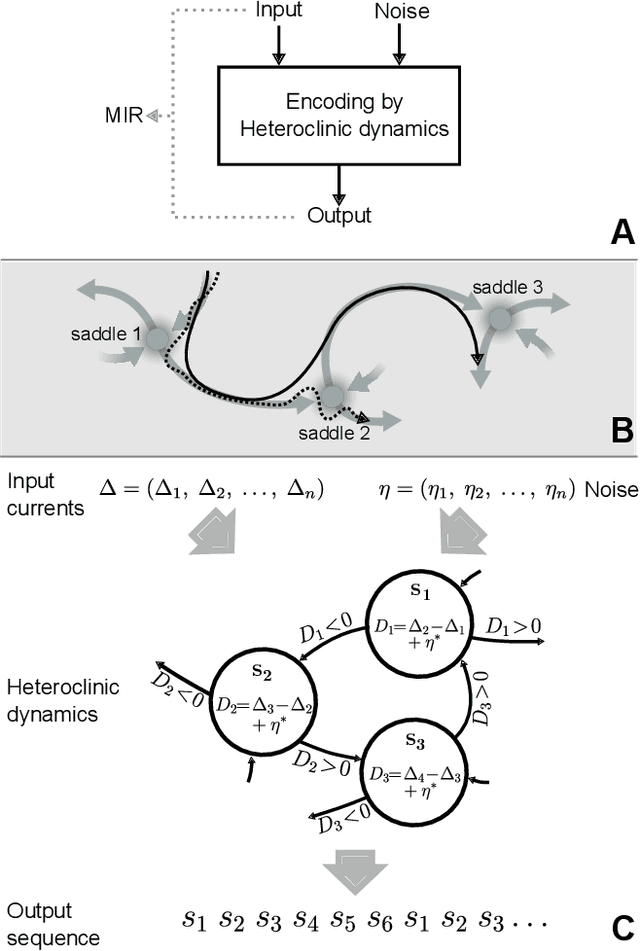
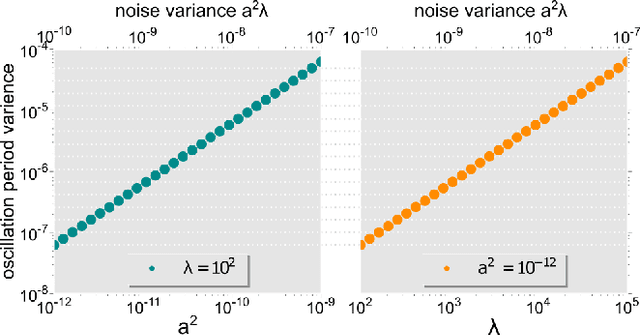
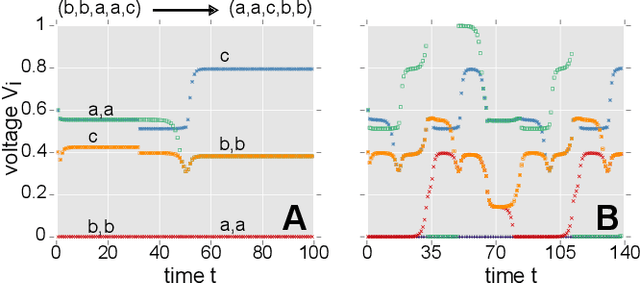
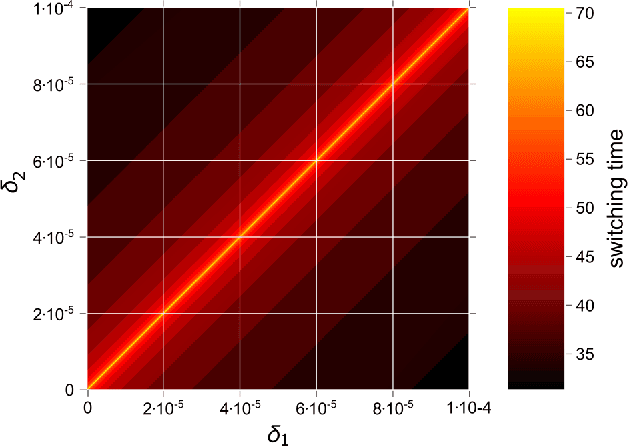
Biological neural systems encode and transmit information as patterns of activity tracing complex trajectories in high-dimensional state-spaces, inspiring alternative paradigms of information processing. Heteroclinic networks, naturally emerging in artificial neural systems, are networks of saddles in state-space that provide a transparent approach to generate complex trajectories via controlled switches among interconnected saddles. External signals induce specific switching sequences, thus dynamically encoding inputs as trajectories. Recent works have focused either on computational aspects of heteroclinic networks, i.e. Heteroclinic Computing, or their stochastic properties under noise. Yet, how well such systems may transmit information remains an open question. Here we investigate the information transmission properties of heteroclinic networks, studying them as communication channels. Choosing a tractable but representative system exhibiting a heteroclinic network, we investigate the mutual information rate (MIR) between input signals and the resulting sequences of states as the level of noise varies. Intriguingly, MIR does not decrease monotonically with increasing noise. Intermediate noise levels indeed maximize the information transmission capacity by promoting an increased yet controlled exploration of the underlying network of states. Complementing standard stochastic resonance, these results highlight the constructive effect of stochastic facilitation (i.e. noise-enhanced information transfer) on heteroclinic communication channels and possibly on more general dynamical systems exhibiting complex trajectories in state-space.

Controlled Perturbation-Induced Switching in Pulse-Coupled Oscillator Networks

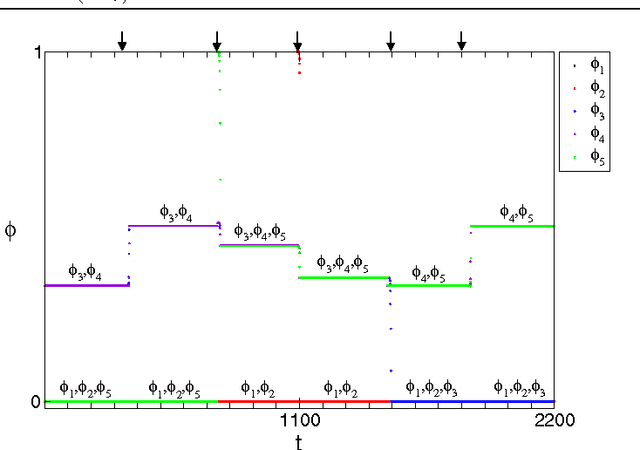
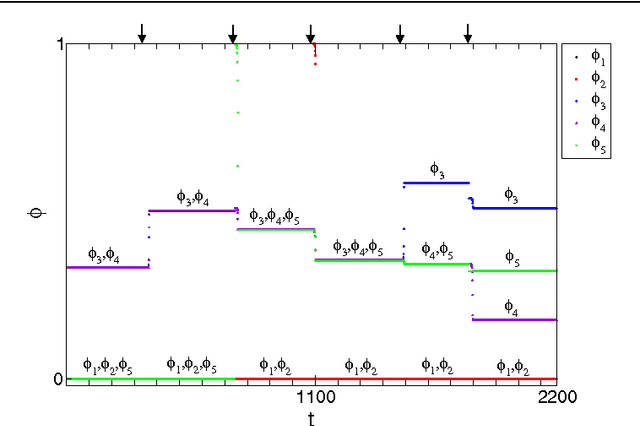
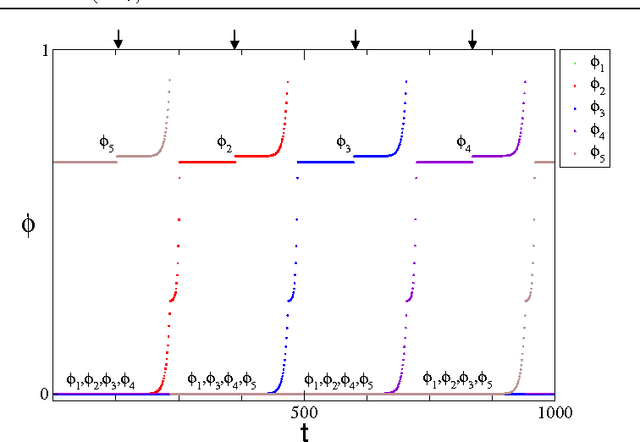
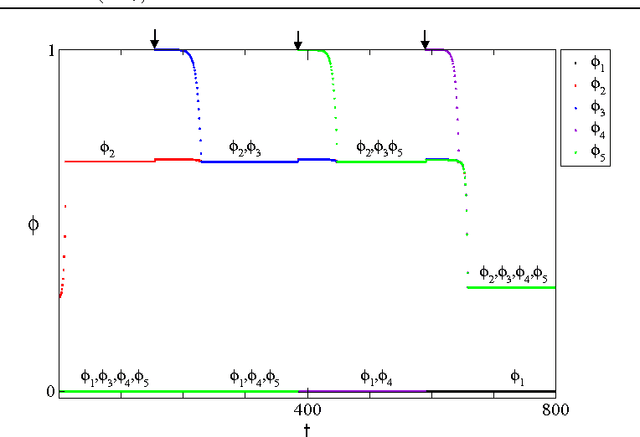
Pulse-coupled systems such as spiking neural networks exhibit nontrivial invariant sets in the form of attracting yet unstable saddle periodic orbits where units are synchronized into groups. Heteroclinic connections between such orbits may in principle support switching processes in those networks and enable novel kinds of neural computations. For small networks of coupled oscillators we here investigate under which conditions and how system symmetry enforces or forbids certain switching transitions that may be induced by perturbations. For networks of five oscillators we derive explicit transition rules that for two cluster symmetries deviate from those known from oscillators coupled continuously in time. A third symmetry yields heteroclinic networks that consist of sets of all unstable attractors with that symmetry and the connections between them. Our results indicate that pulse-coupled systems can reliably generate well-defined sets of complex spatiotemporal patterns that conform to specific transition rules. We briefly discuss possible implications for computation with spiking neural systems.

Inferring network connectivity from event timing patterns

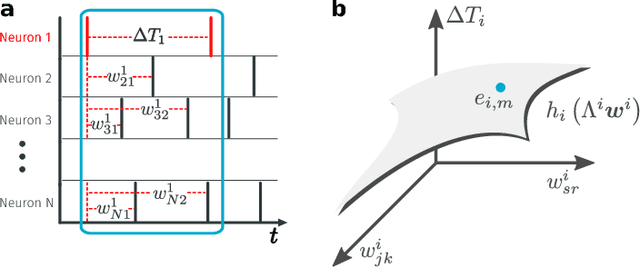
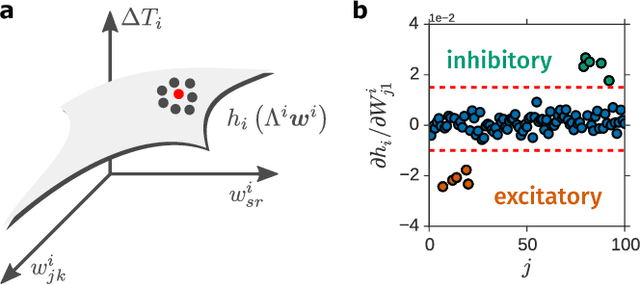
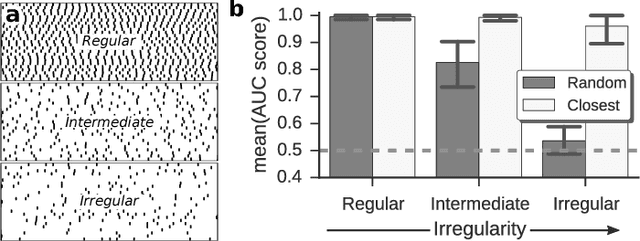
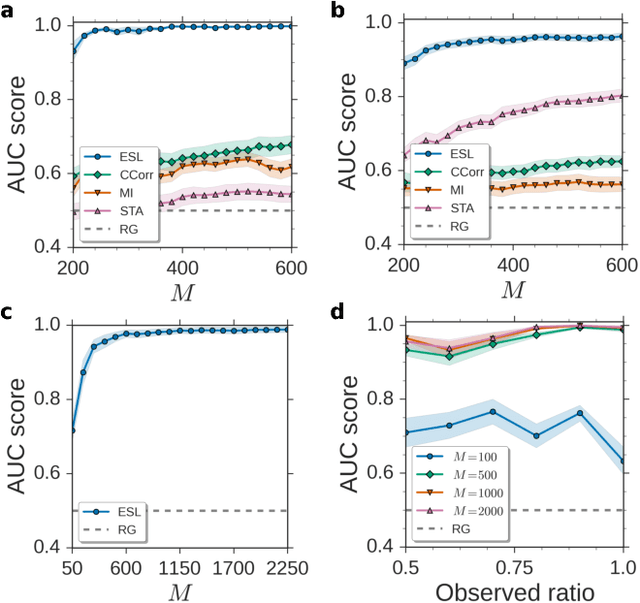
Reconstructing network connectivity from the collective dynamics of a system typically requires access to its complete continuous-time evolution although these are often experimentally inaccessible. Here we propose a theory for revealing physical connectivity of networked systems only from the event time series their intrinsic collective dynamics generate. Representing the patterns of event timings in an event space spanned by inter-event and cross-event intervals, we reveal which other units directly influence the inter-event times of any given unit. For illustration, we linearize an event space mapping constructed from the spiking patterns in model neural circuits to reveal the presence or absence of synapses between any pair of neurons as well as whether the coupling acts in an inhibiting or activating (excitatory) manner. The proposed model-independent reconstruction theory is scalable to larger networks and may thus play an important role in the reconstruction of networks from biology to social science and engineering.

Self-organized adaptation of a simple neural circuit enables complex robot behaviour

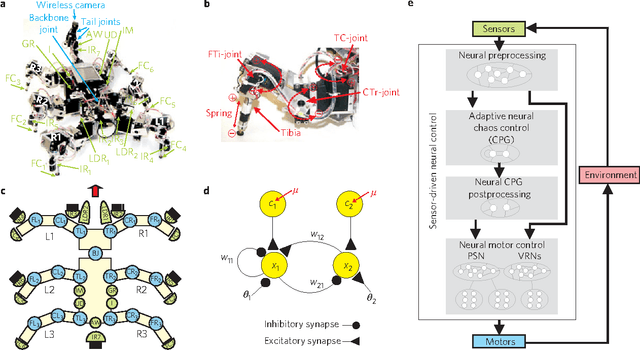
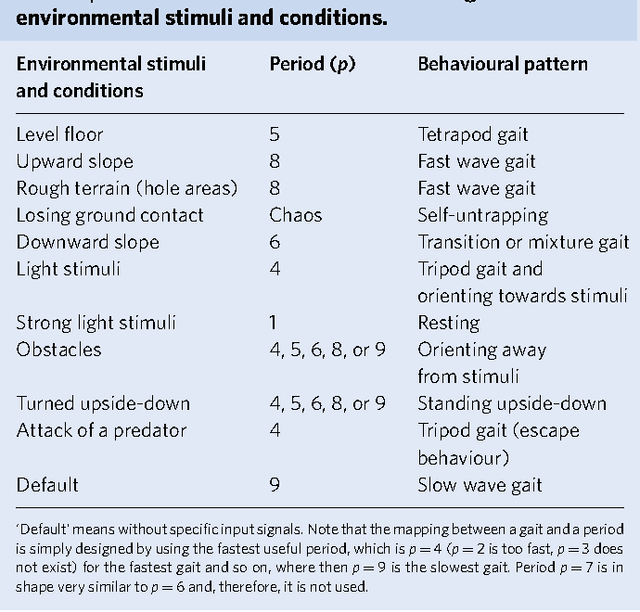
Controlling sensori-motor systems in higher animals or complex robots is a challenging combinatorial problem, because many sensory signals need to be simultaneously coordinated into a broad behavioural spectrum. To rapidly interact with the environment, this control needs to be fast and adaptive. Current robotic solutions operate with limited autonomy and are mostly restricted to few behavioural patterns. Here we introduce chaos control as a new strategy to generate complex behaviour of an autonomous robot. In the presented system, 18 sensors drive 18 motors via a simple neural control circuit, thereby generating 11 basic behavioural patterns (e.g., orienting, taxis, self-protection, various gaits) and their combinations. The control signal quickly and reversibly adapts to new situations and additionally enables learning and synaptic long-term storage of behaviourally useful motor responses. Thus, such neural control provides a powerful yet simple way to self-organize versatile behaviours in autonomous agents with many degrees of freedom.