Geometric constraints improve inference of sparsely observed stochastic dynamics

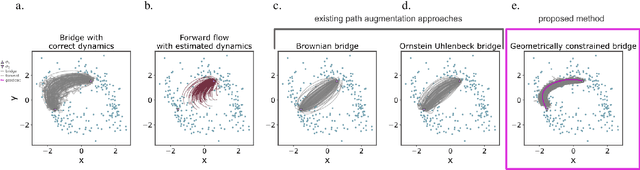
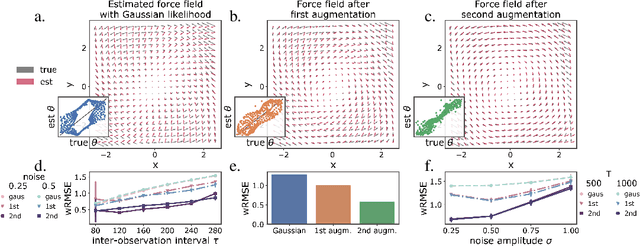
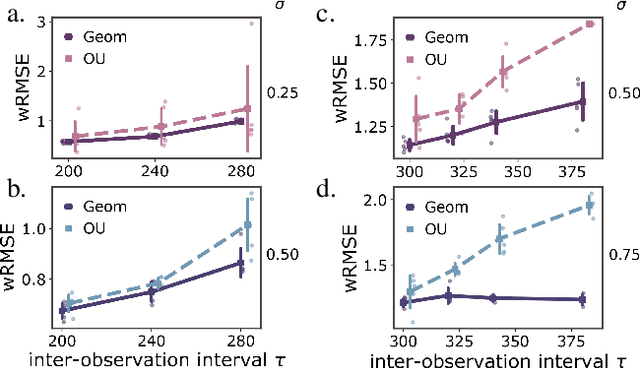
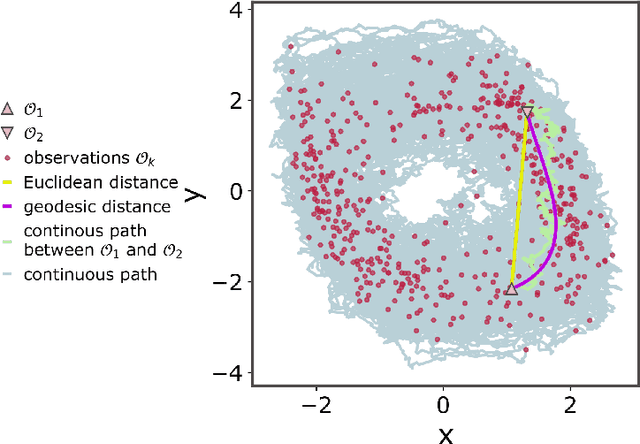
The dynamics of systems of many degrees of freedom evolving on multiple scales are often modeled in terms of stochastic differential equations. Usually the structural form of these equations is unknown and the only manifestation of the system's dynamics are observations at discrete points in time. Despite their widespread use, accurately inferring these systems from sparse-in-time observations remains challenging. Conventional inference methods either focus on the temporal structure of observations, neglecting the geometry of the system's invariant density, or use geometric approximations of the invariant density, which are limited to conservative driving forces. To address these limitations, here, we introduce a novel approach that reconciles these two perspectives. We propose a path augmentation scheme that employs data-driven control to account for the geometry of the invariant system's density. Non-parametric inference on the augmented paths, enables efficient identification of the underlying deterministic forces of systems observed at low sampling rates.

Geometric path augmentation for inference of sparsely observed stochastic nonlinear systems

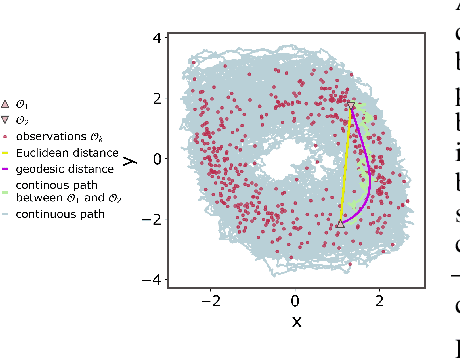
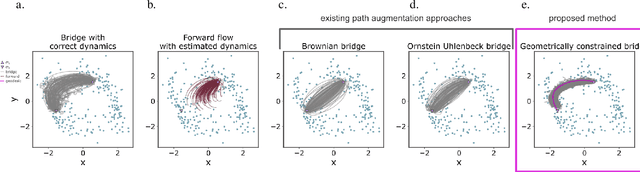
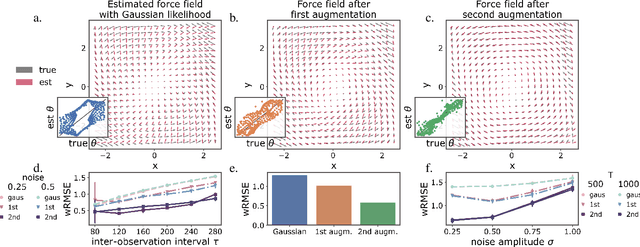
Stochastic evolution equations describing the dynamics of systems under the influence of both deterministic and stochastic forces are prevalent in all fields of science. Yet, identifying these systems from sparse-in-time observations remains still a challenging endeavour. Existing approaches focus either on the temporal structure of the observations by relying on conditional expectations, discarding thereby information ingrained in the geometry of the system's invariant density; or employ geometric approximations of the invariant density, which are nevertheless restricted to systems with conservative forces. Here we propose a method that reconciles these two paradigms. We introduce a new data-driven path augmentation scheme that takes the local observation geometry into account. By employing non-parametric inference on the augmented paths, we can efficiently identify the deterministic driving forces of the underlying system for systems observed at low sampling rates.

Inferring network connectivity from event timing patterns

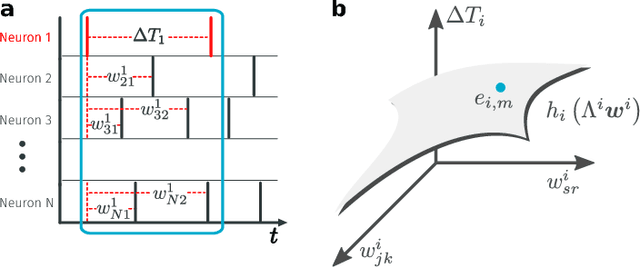
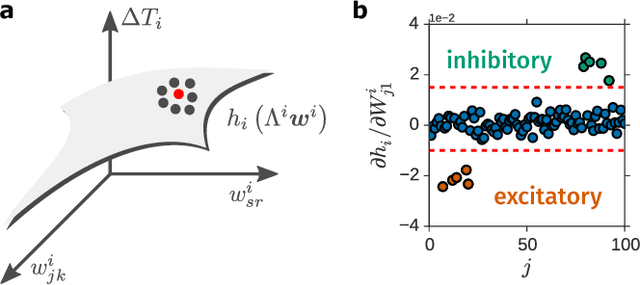
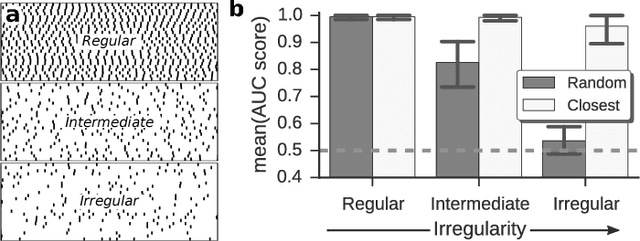
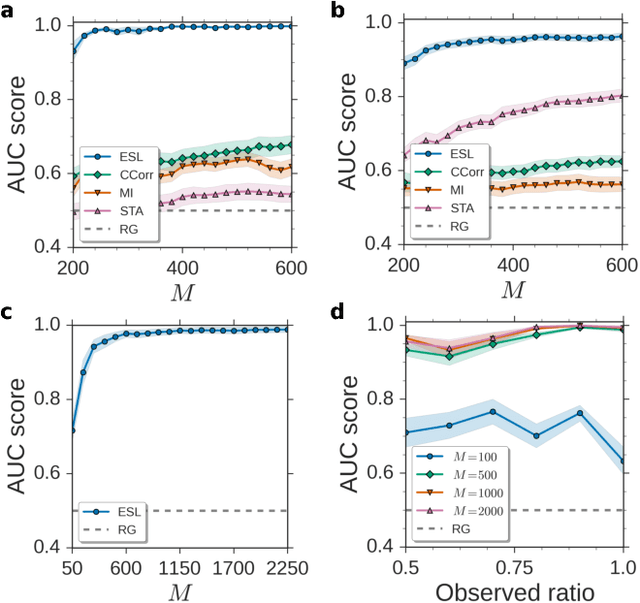
Reconstructing network connectivity from the collective dynamics of a system typically requires access to its complete continuous-time evolution although these are often experimentally inaccessible. Here we propose a theory for revealing physical connectivity of networked systems only from the event time series their intrinsic collective dynamics generate. Representing the patterns of event timings in an event space spanned by inter-event and cross-event intervals, we reveal which other units directly influence the inter-event times of any given unit. For illustration, we linearize an event space mapping constructed from the spiking patterns in model neural circuits to reveal the presence or absence of synapses between any pair of neurons as well as whether the coupling acts in an inhibiting or activating (excitatory) manner. The proposed model-independent reconstruction theory is scalable to larger networks and may thus play an important role in the reconstruction of networks from biology to social science and engineering.