Adaptive versus Standard Descent Methods and Robustness Against Adversarial Examples

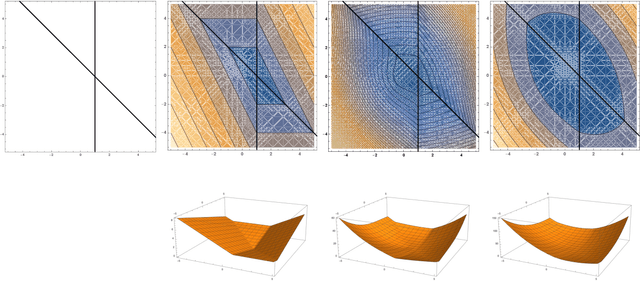
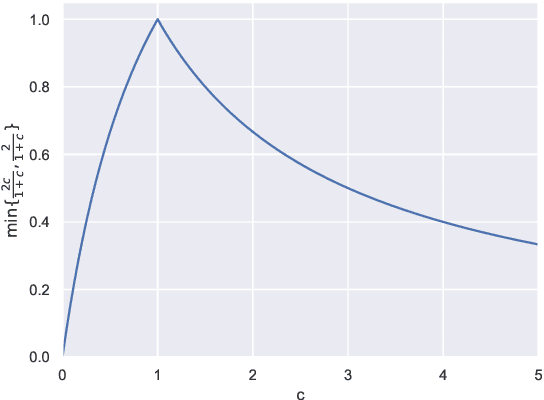
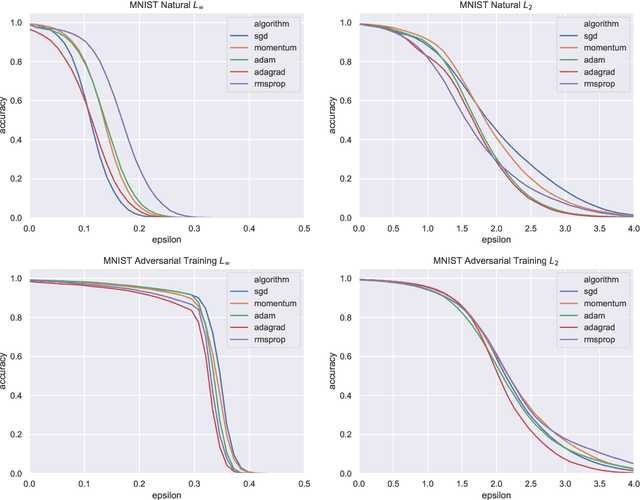
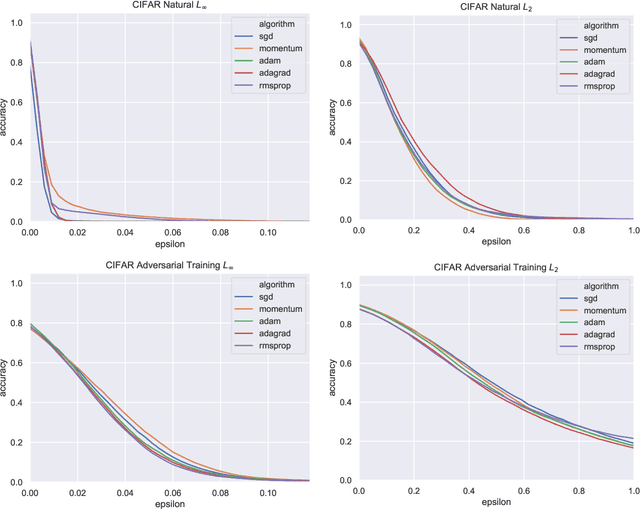
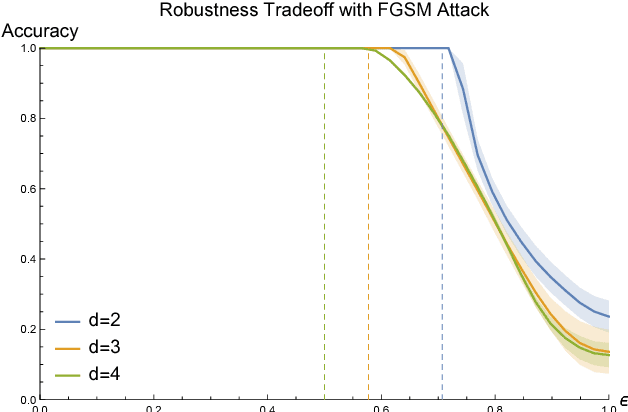
Adversarial examples are a pervasive phenomenon of machine learning models where seemingly imperceptible perturbations to the input lead to misclassifications for otherwise statistically accurate models. In this paper we study how the choice of optimization algorithm influences the robustness of the resulting classifier to adversarial examples. Specifically we show an example of a learning problem for which the solution found by adaptive optimization algorithms exhibits qualitatively worse robustness properties against both $L_{2}$- and $L_{\infty}$-adversaries than the solution found by non-adaptive algorithms. Then we fully characterize the geometry of the loss landscape of $L_{2}$-adversarial training in least-squares linear regression. The geometry of the loss landscape is subtle and has important consequences for optimization algorithms. Finally we provide experimental evidence which suggests that non-adaptive methods consistently produce more robust models than adaptive methods.

Adversarial Training with Voronoi Constraints

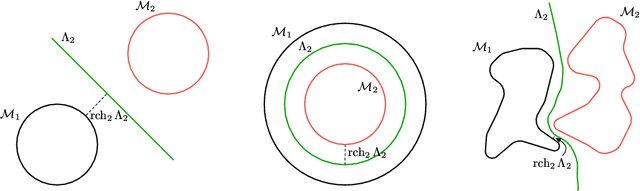
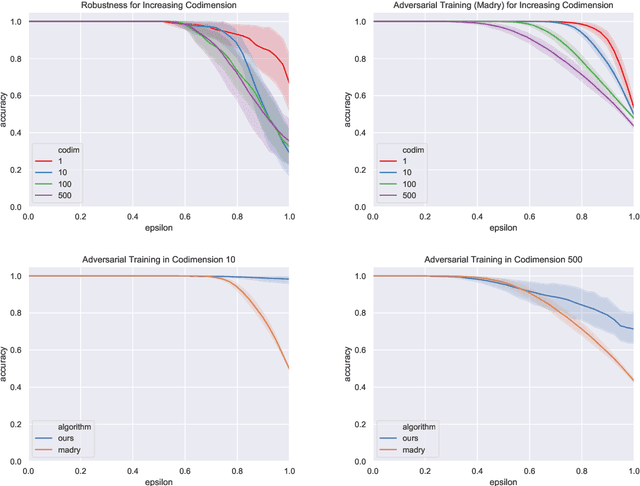
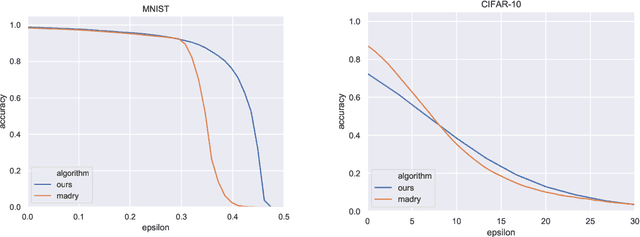
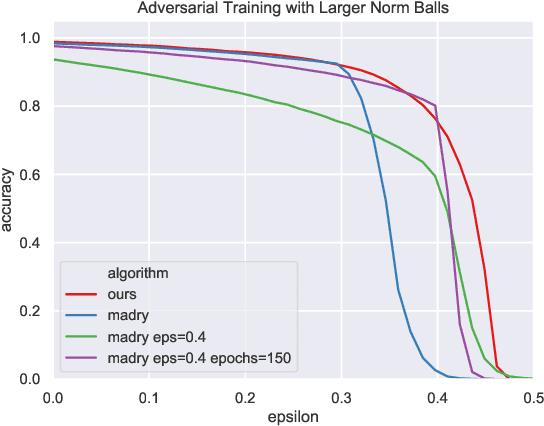
Adversarial examples are a pervasive phenomenon of machine learning models where seemingly imperceptible perturbations to the input lead to misclassifications for otherwise statistically accurate models. We propose a geometric framework, drawing on tools from the manifold reconstruction literature, to analyze the high-dimensional geometry of adversarial examples. In particular, we highlight the importance of codimension: for low-dimensional data manifolds embedded in high-dimensional space there are many directions off the manifold in which an adversary could construct adversarial examples. Adversarial examples are a natural consequence of learning a decision boundary that classifies the low-dimensional data manifold well, but classifies points near the manifold incorrectly. Using our geometric framework we prove that adversarial training is sample inefficient, and show sufficient sampling conditions under which nearest neighbor classifiers and ball-based adversarial training are robust. Finally we introduce adversarial training with Voronoi constraints, which replaces the norm ball constraint with the Voronoi cell for each point in the training set. We show that adversarial training with Voronoi constraints produces robust models which significantly improve over the state-of-the-art on MNIST and are competitive on CIFAR-10.

On the Geometry of Adversarial Examples

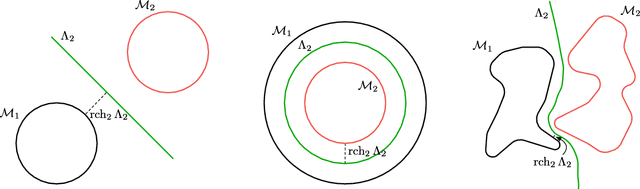
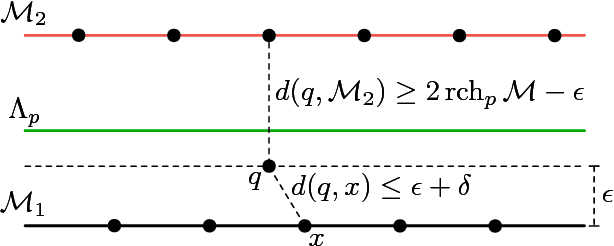
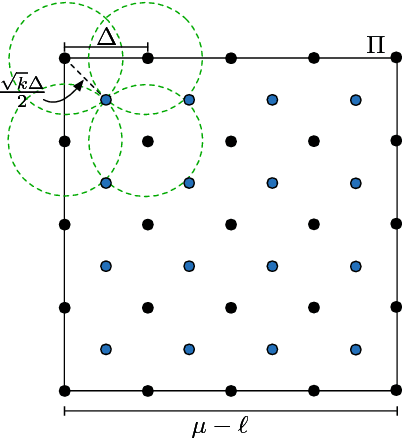
Adversarial examples are a pervasive phenomenon of machine learning models where seemingly imperceptible perturbations to the input lead to misclassifications for otherwise statistically accurate models. We propose a geometric framework, drawing on tools from the manifold reconstruction literature, to analyze the high-dimensional geometry of adversarial examples. In particular, we highlight the importance of codimension: for low-dimensional data manifolds embedded in high-dimensional space there are many directions off the manifold in which to construct adversarial examples. Adversarial examples are a natural consequence of learning a decision boundary that classifies the low-dimensional data manifold well, but classifies points near the manifold incorrectly. Using our geometric framework we prove (1) a tradeoff between robustness under different norms, (2) that adversarial training in balls around the data is sample inefficient, and (3) sufficient sampling conditions under which nearest neighbor classifiers and ball-based adversarial training are robust.

Learning Compact Geometric Features

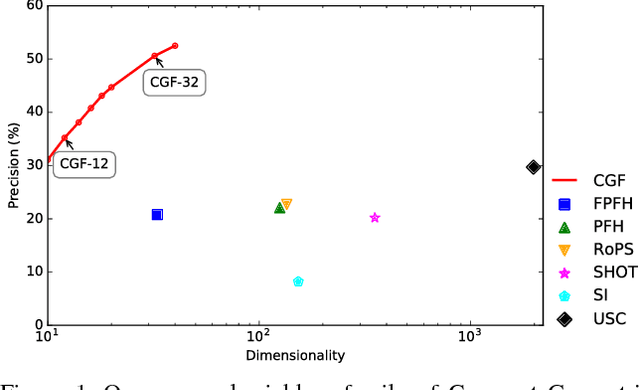
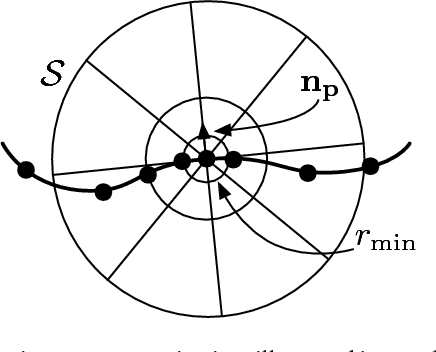
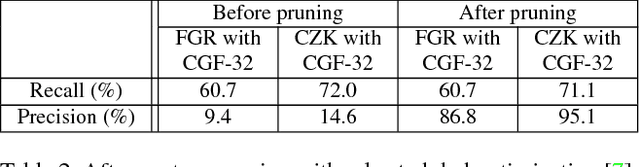
We present an approach to learning features that represent the local geometry around a point in an unstructured point cloud. Such features play a central role in geometric registration, which supports diverse applications in robotics and 3D vision. Current state-of-the-art local features for unstructured point clouds have been manually crafted and none combines the desirable properties of precision, compactness, and robustness. We show that features with these properties can be learned from data, by optimizing deep networks that map high-dimensional histograms into low-dimensional Euclidean spaces. The presented approach yields a family of features, parameterized by dimension, that are both more compact and more accurate than existing descriptors.