Adversarial Training with Voronoi Constraints
Paper and Code
May 02, 2019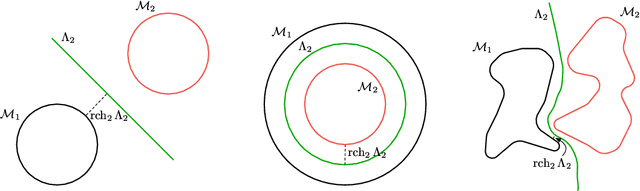

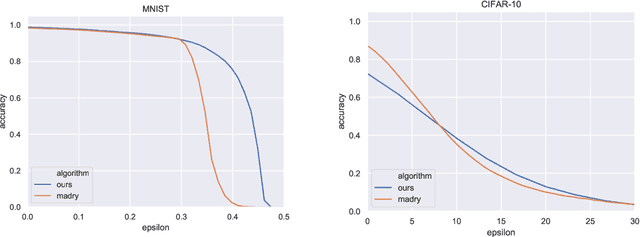
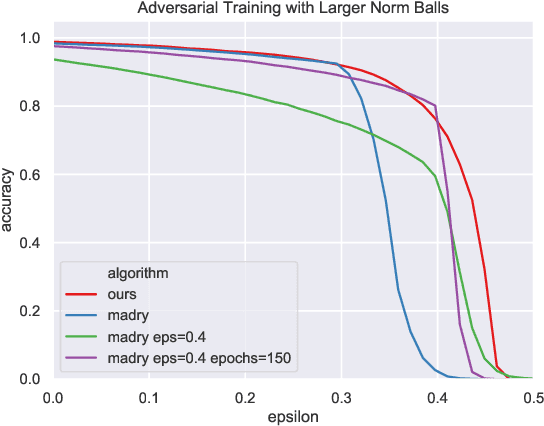
Adversarial examples are a pervasive phenomenon of machine learning models where seemingly imperceptible perturbations to the input lead to misclassifications for otherwise statistically accurate models. We propose a geometric framework, drawing on tools from the manifold reconstruction literature, to analyze the high-dimensional geometry of adversarial examples. In particular, we highlight the importance of codimension: for low-dimensional data manifolds embedded in high-dimensional space there are many directions off the manifold in which an adversary could construct adversarial examples. Adversarial examples are a natural consequence of learning a decision boundary that classifies the low-dimensional data manifold well, but classifies points near the manifold incorrectly. Using our geometric framework we prove that adversarial training is sample inefficient, and show sufficient sampling conditions under which nearest neighbor classifiers and ball-based adversarial training are robust. Finally we introduce adversarial training with Voronoi constraints, which replaces the norm ball constraint with the Voronoi cell for each point in the training set. We show that adversarial training with Voronoi constraints produces robust models which significantly improve over the state-of-the-art on MNIST and are competitive on CIFAR-10.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge