Adaptive versus Standard Descent Methods and Robustness Against Adversarial Examples
Paper and Code
Nov 09, 2019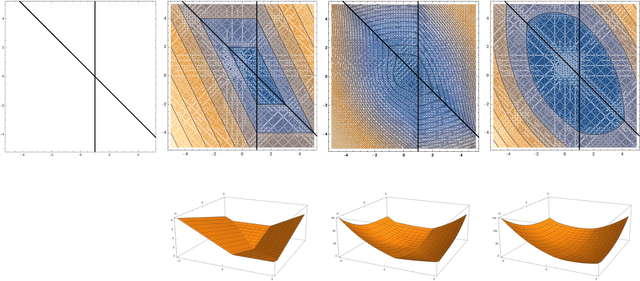
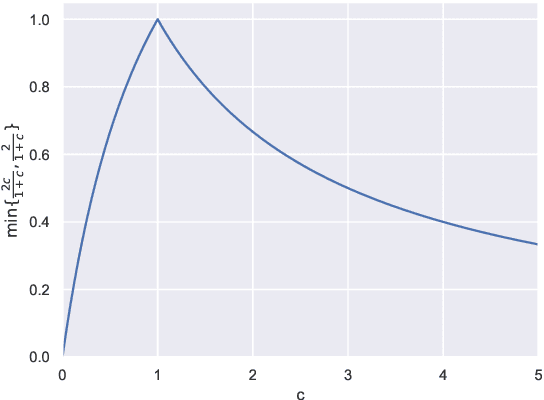
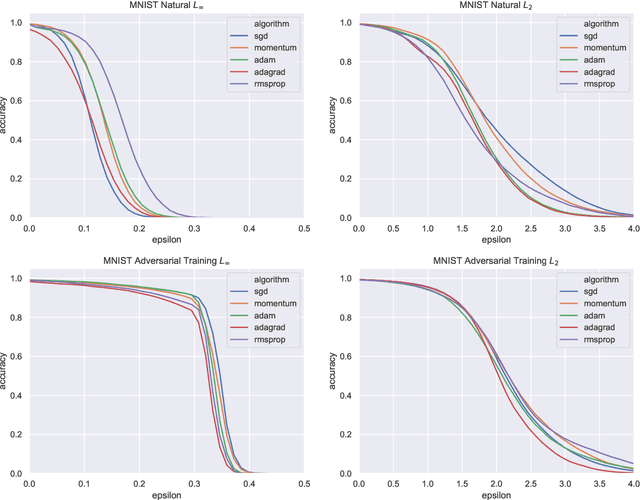
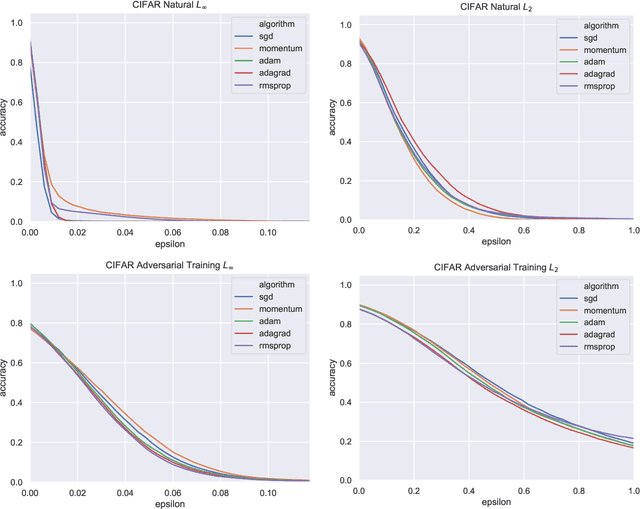
Adversarial examples are a pervasive phenomenon of machine learning models where seemingly imperceptible perturbations to the input lead to misclassifications for otherwise statistically accurate models. In this paper we study how the choice of optimization algorithm influences the robustness of the resulting classifier to adversarial examples. Specifically we show an example of a learning problem for which the solution found by adaptive optimization algorithms exhibits qualitatively worse robustness properties against both $L_{2}$- and $L_{\infty}$-adversaries than the solution found by non-adaptive algorithms. Then we fully characterize the geometry of the loss landscape of $L_{2}$-adversarial training in least-squares linear regression. The geometry of the loss landscape is subtle and has important consequences for optimization algorithms. Finally we provide experimental evidence which suggests that non-adaptive methods consistently produce more robust models than adaptive methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge