Modeling High-Resolution Spatio-Temporal Wind with Deep Echo State Networks and Stochastic Partial Differential Equations

In the past decades, clean and renewable energy has gained increasing attention due to a global effort on carbon footprint reduction. In particular, Saudi Arabia is gradually shifting its energy portfolio from an exclusive use of oil to a reliance on renewable energy, and, in particular, wind. Modeling wind for assessing potential energy output in a country as large, geographically diverse and understudied as Saudi Arabia is a challenge which implies highly non-linear dynamic structures in both space and time. To address this, we propose a spatio-temporal model whose spatial information is first reduced via an energy distance-based approach and then its dynamical behavior is informed by a sparse and stochastic recurrent neural network (Echo State Network). Finally, the full spatial data is reconstructed by means of a non-stationary stochastic partial differential equation-based approach. Our model can capture the fine scale wind structure and produce more accurate forecasts of both wind speed and energy in lead times of interest for energy grid management and save annually as much as one million dollar against the closest competitive model.

A Generalized Unified Skew-Normal Process with Neural Bayes Inference

In recent decades, statisticians have been increasingly encountering spatial data that exhibit non-Gaussian behaviors such as asymmetry and heavy-tailedness. As a result, the assumptions of symmetry and fixed tail weight in Gaussian processes have become restrictive and may fail to capture the intrinsic properties of the data. To address the limitations of the Gaussian models, a variety of skewed models has been proposed, of which the popularity has grown rapidly. These skewed models introduce parameters that govern skewness and tail weight. Among various proposals in the literature, unified skewed distributions, such as the Unified Skew-Normal (SUN), have received considerable attention. In this work, we revisit a more concise and intepretable re-parameterization of the SUN distribution and apply the distribution to random fields by constructing a generalized unified skew-normal (GSUN) spatial process. We demonstrate { that the GSUN is a valid spatial process by showing its vanishing correlation in large distances} and provide the corresponding spatial interpolation method. In addition, we develop an inference mechanism for the GSUN process using the concept of neural Bayes estimators with deep graphical attention networks (GATs) and encoder transformer. We show the superiority of our proposed estimator over the conventional CNN-based architectures regarding stability and accuracy by means of a simulation study and application to Pb-contaminated soil data. Furthermore, we show that the GSUN process is different from the conventional Gaussian processes and Tukey g-and-h processes, through the probability integral transform (PIT).

Efficient Large-scale Nonstationary Spatial Covariance Function Estimation Using Convolutional Neural Networks

Spatial processes observed in various fields, such as climate and environmental science, often occur on a large scale and demonstrate spatial nonstationarity. Fitting a Gaussian process with a nonstationary Mat\'ern covariance is challenging. Previous studies in the literature have tackled this challenge by employing spatial partitioning techniques to estimate the parameters that vary spatially in the covariance function. The selection of partitions is an important consideration, but it is often subjective and lacks a data-driven approach. To address this issue, in this study, we utilize the power of Convolutional Neural Networks (ConvNets) to derive subregions from the nonstationary data. We employ a selection mechanism to identify subregions that exhibit similar behavior to stationary fields. In order to distinguish between stationary and nonstationary random fields, we conducted training on ConvNet using various simulated data. These simulations are generated from Gaussian processes with Mat\'ern covariance models under a wide range of parameter settings, ensuring adequate representation of both stationary and nonstationary spatial data. We assess the performance of the proposed method with synthetic and real datasets at a large scale. The results revealed enhanced accuracy in parameter estimations when relying on ConvNet-based partition compared to traditional user-defined approaches.

Scalable Gaussian-process regression and variable selection using Vecchia approximations

Gaussian process (GP) regression is a flexible, nonparametric approach to regression that naturally quantifies uncertainty. In many applications, the number of responses and covariates are both large, and a goal is to select covariates that are related to the response. For this setting, we propose a novel, scalable algorithm, coined VGPR, which optimizes a penalized GP log-likelihood based on the Vecchia GP approximation, an ordered conditional approximation from spatial statistics that implies a sparse Cholesky factor of the precision matrix. We traverse the regularization path from strong to weak penalization, sequentially adding candidate covariates based on the gradient of the log-likelihood and deselecting irrelevant covariates via a new quadratic constrained coordinate descent algorithm. We propose Vecchia-based mini-batch subsampling, which provides unbiased gradient estimators. The resulting procedure is scalable to millions of responses and thousands of covariates. Theoretical analysis and numerical studies demonstrate the improved scalability and accuracy relative to existing methods.

An Outlyingness Matrix for Multivariate Functional Data Classification

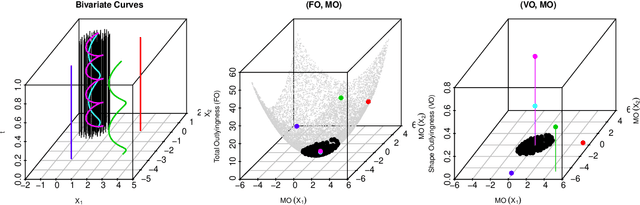
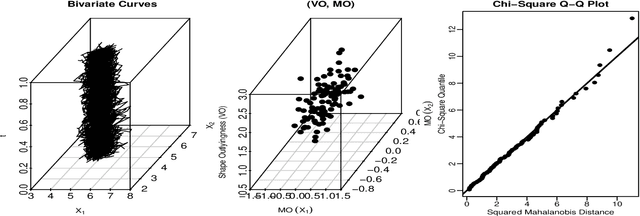
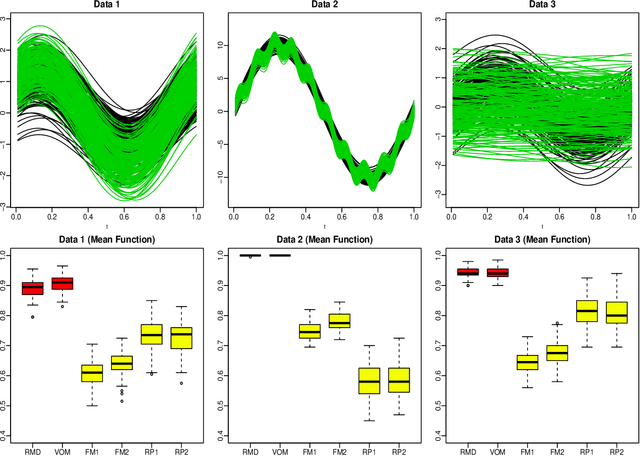
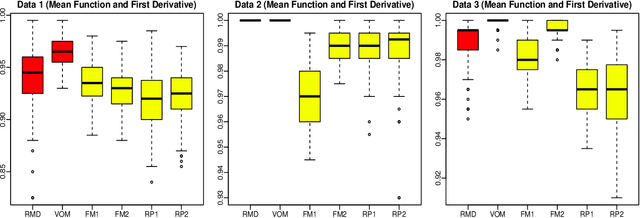
The classification of multivariate functional data is an important task in scientific research. Unlike point-wise data, functional data are usually classified by their shapes rather than by their scales. We define an outlyingness matrix by extending directional outlyingness, an effective measure of the shape variation of curves that combines the direction of outlyingness with conventional depth. We propose two classifiers based on directional outlyingness and the outlyingness matrix, respectively. Our classifiers provide better performance compared with existing depth-based classifiers when applied on both univariate and multivariate functional data from simulation studies. We also test our methods on two data problems: speech recognition and gesture classification, and obtain results that are consistent with the findings from the simulated data.