Implementation and Analysis of GPU Algorithms for Vecchia Approximation

Gaussian Processes have become an indispensable part of the spatial statistician's toolbox but are unsuitable for analyzing large dataset because of the significant time and memory needed to fit the associated model exactly. Vecchia Approximation is widely used to reduce the computational complexity and can be calculated with embarrassingly parallel algorithms. While multi-core software has been developed for Vecchia Approximation, such as the GpGp R package, software designed to run on graphics processing units (GPU) is lacking, despite the tremendous success GPUs have had in statistics and machine learning. We compare three different ways to implement Vecchia Approximation on a GPU: two of which are similar to methods used for other Gaussian Process approximations and one that is new. The impact of memory type on performance is investigated and the final method is optimized accordingly. We show that our new method outperforms the other two and then present it in the GpGpU R package. We compare GpGpU to existing multi-core and GPU-accelerated software by fitting Gaussian Process models on various datasets, including a large spatial-temporal dataset of $n>10^6$ points collected from an earth-observing satellite. Our results show that GpGpU achieves faster runtimes and better predictive accuracy.

Scalable Gaussian-process regression and variable selection using Vecchia approximations

Gaussian process (GP) regression is a flexible, nonparametric approach to regression that naturally quantifies uncertainty. In many applications, the number of responses and covariates are both large, and a goal is to select covariates that are related to the response. For this setting, we propose a novel, scalable algorithm, coined VGPR, which optimizes a penalized GP log-likelihood based on the Vecchia GP approximation, an ordered conditional approximation from spatial statistics that implies a sparse Cholesky factor of the precision matrix. We traverse the regularization path from strong to weak penalization, sequentially adding candidate covariates based on the gradient of the log-likelihood and deselecting irrelevant covariates via a new quadratic constrained coordinate descent algorithm. We propose Vecchia-based mini-batch subsampling, which provides unbiased gradient estimators. The resulting procedure is scalable to millions of responses and thousands of covariates. Theoretical analysis and numerical studies demonstrate the improved scalability and accuracy relative to existing methods.

Scaled Vecchia approximation for fast computer-model emulation

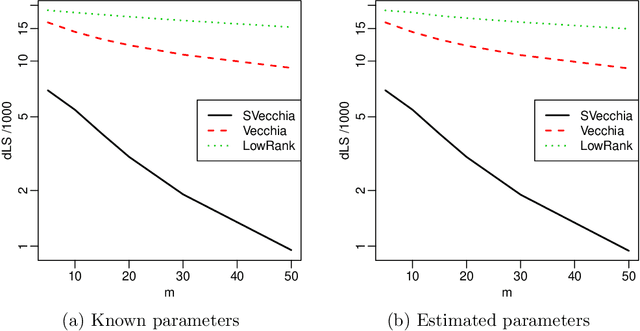
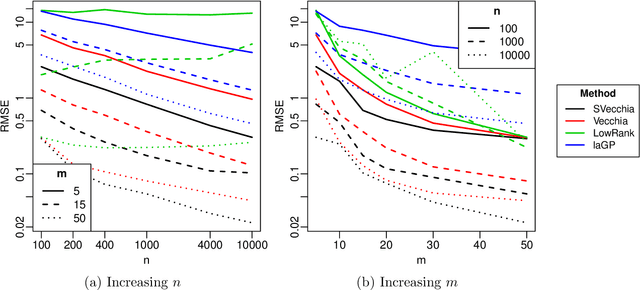
Many scientific phenomena are studied using computer experiments consisting of multiple runs of a computer model while varying the input settings. Gaussian processes (GPs) are a popular tool for the analysis of computer experiments, enabling interpolation between input settings, but direct GP inference is computationally infeasible for large datasets. We adapt and extend a powerful class of GP methods from spatial statistics to enable the scalable analysis and emulation of large computer experiments. Specifically, we apply Vecchia's ordered conditional approximation in a transformed input space, with each input scaled according to how strongly it relates to the computer-model response. The scaling is learned from the data, by estimating parameters in the GP covariance function using Fisher scoring. Our methods are highly scalable, enabling estimation, joint prediction and simulation in near-linear time in the number of model runs. In several numerical examples, our approach substantially outperformed existing methods.

Inverses of Matern Covariances on Grids

We conduct a theoretical and numerical study of the aliased spectral densities and inverse operators of Mat\'ern covariance functions on regular grids. We apply our results to provide clarity on the properties of a popular approximation based on stochastic partial differential equations; we find that it can approximate the aliased spectral density and the covariance operator well as the grid spacing goes to zero, but it does not provide increasingly accurate approximations to the inverse operator as the grid spacing goes to zero. If a sparse approximation to the inverse is desired, we suggest instead to select a KL-divergence-minimizing sparse approximation and demonstrate in simulations that these sparse approximations deliver accurate Mat\'ern parameter estimates, while the SPDE approximation over-estimates spatial dependence.

Gaussian Process Learning via Fisher Scoring of Vecchia's Approximation

We derive a single pass algorithm for computing the gradient and Fisher information of Vecchia's Gaussian process loglikelihood approximation, which provides a computationally efficient means for applying the Fisher scoring algorithm for maximizing the loglikelihood. The advantages of the optimization techniques are demonstrated in numerical examples and in an application to Argo ocean temperature data. The new methods are more accurate and much faster than an optimization method that uses only function evaluations, especially when the covariance function has many parameters. This allows practitioners to fit nonstationary models to large spatial and spatial-temporal datasets.