Quantifying Uncertainty In Wide Two-Layer Neural Networks: On The Law Of The Limiting Fluctuation Process

Uncertainty quantification in neural networks prediction is a main issue for usual applications. Our approach seeks at reducing computation costs by directly evaluating uncertainty using PDE's information on the asymptotic variance, rather than the deep ensemble method which may be seen as a Monte Carlo estimation of the prediction, requiring the training of multiple networks. We thus study the law of the limiting process describing the random fluctuations around the mean-field limit of wide two-layer neural networks trained by stochastic gradient descent in a weak-noise regime. Building on a recent trajectorial central limit theorem, in which this limit is characterized as the weak solution of a linear stochastic evolution equation, we identify its law explicitly. More precisely, we show that it is a centered Gaussian process in the dual of a weighted Sobolev space, and we derive a closed covariance representation for the finite-dimensional distributions obtained by testing it against smooth functions. This covariance is expressed through the solution of a backward transport equation with a nonlocal source term, whose coefficients are driven by the mean-field trajectory. As a consequence, by testing against the activation function at a fixed input, we obtain an expression for the limiting variance of the corresponding network-output fluctuations. We illustrate this result numerically on a one-dimensional regression example.

Central Limit Theorem for Bayesian Neural Network trained with Variational Inference

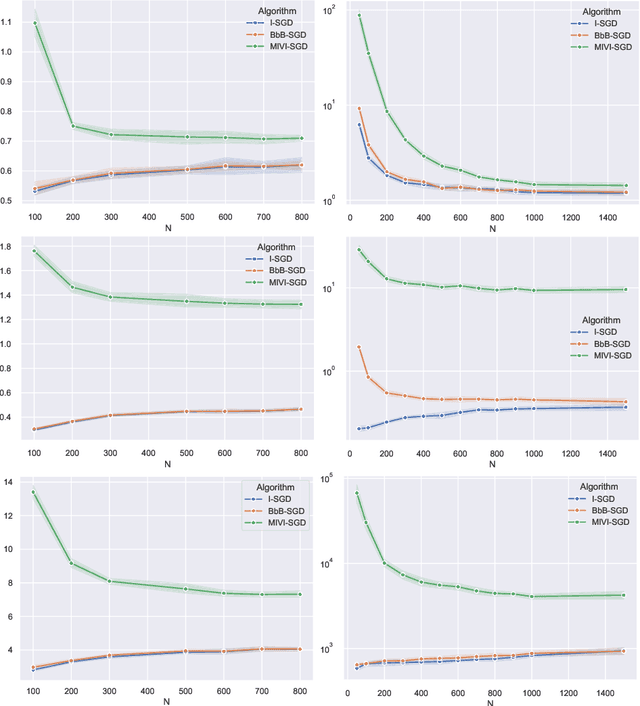
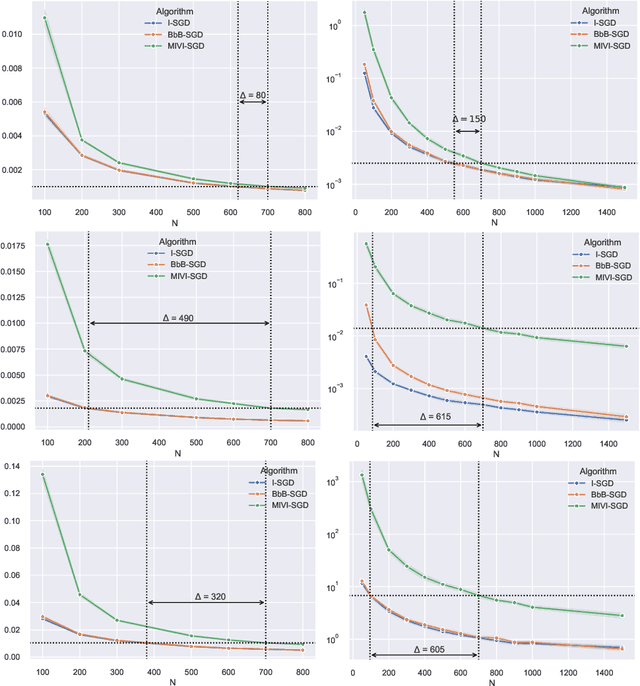
In this paper, we rigorously derive Central Limit Theorems (CLT) for Bayesian two-layerneural networks in the infinite-width limit and trained by variational inference on a regression task. The different networks are trained via different maximization schemes of the regularized evidence lower bound: (i) the idealized case with exact estimation of a multiple Gaussian integral from the reparametrization trick, (ii) a minibatch scheme using Monte Carlo sampling, commonly known as Bayes-by-Backprop, and (iii) a computationally cheaper algorithm named Minimal VI. The latter was recently introduced by leveraging the information obtained at the level of the mean-field limit. Laws of large numbers are already rigorously proven for the three schemes that admits the same asymptotic limit. By deriving CLT, this work shows that the idealized and Bayes-by-Backprop schemes have similar fluctuation behavior, that is different from the Minimal VI one. Numerical experiments then illustrate that the Minimal VI scheme is still more efficient, in spite of bigger variances, thanks to its important gain in computational complexity.

Law of Large Numbers for Bayesian two-layer Neural Network trained with Variational Inference

We provide a rigorous analysis of training by variational inference (VI) of Bayesian neural networks in the two-layer and infinite-width case. We consider a regression problem with a regularized evidence lower bound (ELBO) which is decomposed into the expected log-likelihood of the data and the Kullback-Leibler (KL) divergence between the a priori distribution and the variational posterior. With an appropriate weighting of the KL, we prove a law of large numbers for three different training schemes: (i) the idealized case with exact estimation of a multiple Gaussian integral from the reparametrization trick, (ii) a minibatch scheme using Monte Carlo sampling, commonly known as Bayes by Backprop, and (iii) a new and computationally cheaper algorithm which we introduce as Minimal VI. An important result is that all methods converge to the same mean-field limit. Finally, we illustrate our results numerically and discuss the need for the derivation of a central limit theorem.

Fixed-kinetic Neural Hamiltonian Flows for enhanced interpretability and reduced complexity

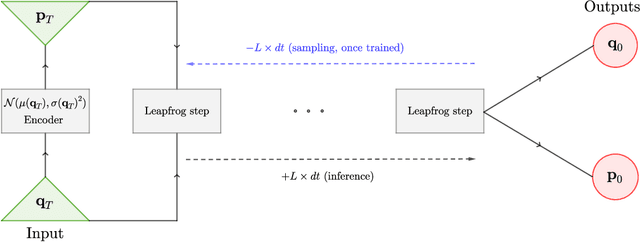
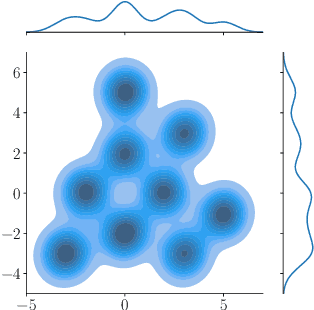
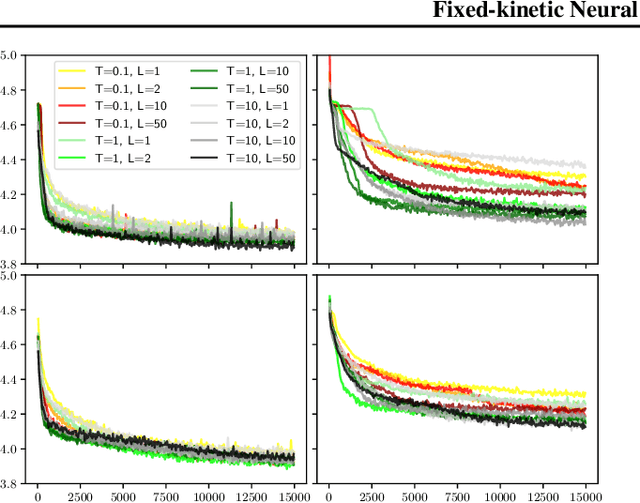
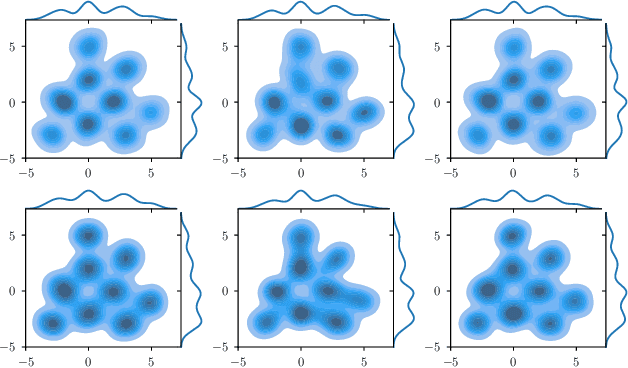
Normalizing Flows (NF) are Generative models which are particularly robust and allow for exact sampling of the learned distribution. They however require the design of an invertible mapping, whose Jacobian determinant has to be computable. Recently introduced, Neural Hamiltonian Flows (NHF) are based on Hamiltonian dynamics-based Flows, which are continuous, volume-preserving and invertible and thus make for natural candidates for robust NF architectures. In particular, their similarity to classical Mechanics could lead to easier interpretability of the learned mapping. However, despite being Physics-inspired architectures, the originally introduced NHF architecture still poses a challenge to interpretability. For this reason, in this work, we introduce a fixed kinetic energy version of the NHF model. Inspired by physics, our approach improves interpretability and requires less parameters than previously proposed architectures. We then study the robustness of the NHF architectures to the choice of hyperparameters. We analyze the impact of the number of leapfrog steps, the integration time and the number of neurons per hidden layer, as well as the choice of prior distribution, on sampling a multimodal 2D mixture. The NHF architecture is robust to these choices, especially the fixed-kinetic energy model. Finally, we adapt NHF to the context of Bayesian inference and illustrate our method on sampling the posterior distribution of two cosmological parameters knowing type Ia supernovae observations.