On modeling vagueness and uncertainty in data-to-text systems through fuzzy sets

Vagueness and uncertainty management is counted among one of the challenges that remain unresolved in systems that generate texts from non-linguistic data, known as data-to-text systems. In the last decade, work in fuzzy linguistic summarization and description of data has raised the interest of using fuzzy sets to model and manage the imprecision of human language in data-to-text systems. However, despite some research in this direction, there has not been an actual clear discussion and justification on how fuzzy sets can contribute to data-to-text for modeling vagueness and uncertainty in words and expressions. This paper intends to bridge this gap by answering the following questions: What does vagueness mean in fuzzy sets theory? What does vagueness mean in data-to-text contexts? In what ways can fuzzy sets theory contribute to improve data-to-text systems? What are the challenges that researchers from both disciplines need to address for a successful integration of fuzzy sets into data-to-text systems? In what cases should the use of fuzzy sets be avoided in D2T? For this, we review and discuss the state of the art of vagueness modeling in natural language generation and data-to-text, describe potential and actual usages of fuzzy sets in data-to-text contexts, and provide some additional insights about the engineering of data-to-text systems that make use of fuzzy set-based techniques.

Characterizing Quantifier Fuzzification Mechanisms: a behavioral guide for practical applications

Important advances have been made in the fuzzy quantification field. Nevertheless, some problems remain when we face the decision of selecting the most convenient model for a specific application. In the literature, several desirable adequacy properties have been proposed, but theoretical limits impede quantification models from simultaneously fulfilling every adequacy property that has been defined. Besides, the complexity of model definitions and adequacy properties makes very difficult for real users to understand the particularities of the different models that have been presented. In this work we will present several criteria conceived to help in the process of selecting the most adequate Quantifier Fuzzification Mechanisms for specific practical applications. In addition, some of the best known well-behaved models will be compared against this list of criteria. Based on this analysis, some guidance to choose fuzzy quantification models for practical applications will be provided.

On the analysis of set-based fuzzy quantified reasoning using classical syllogistics

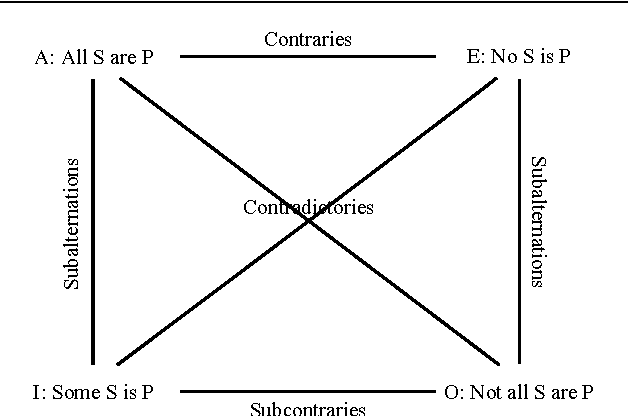
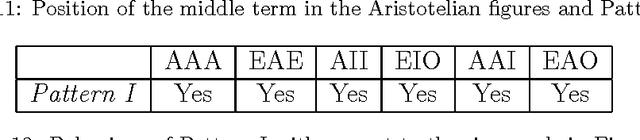
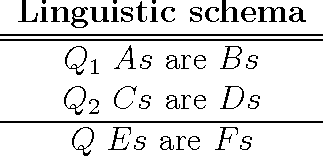
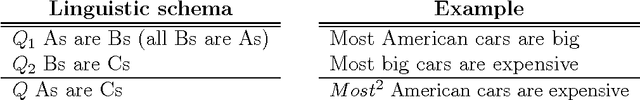
Syllogism is a type of deductive reasoning involving quantified statements. The syllogistic reasoning scheme in the classical Aristotelian framework involves three crisp term sets and four linguistic quantifiers, for which the main support is the linguistic properties of the quantifiers. A number of fuzzy approaches for defining an approximate syllogism have been proposed for which the main support is cardinality calculus. In this paper we analyze fuzzy syllogistic models previously described by Zadeh and Dubois et al. and compare their behavior with that of the classical Aristotelian framework to check which of the 24 classical valid syllogistic reasoning patterns or moods are particular crisp cases of these fuzzy approaches. This allows us to assess to what extent these approaches can be considered as either plausible extensions of the classical crisp syllogism or a basis for a general approach to the problem of approximate syllogism.

A Fuzzy Syllogistic Reasoning Schema for Generalized Quantifiers

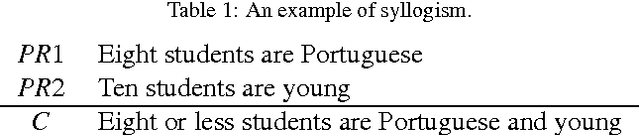
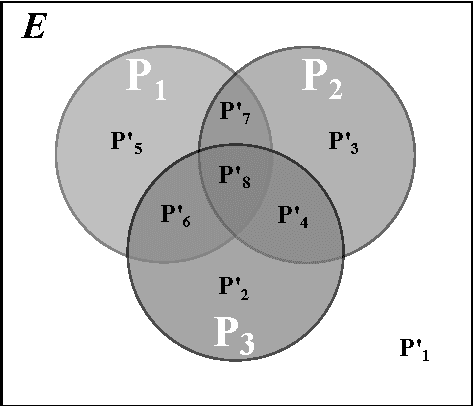
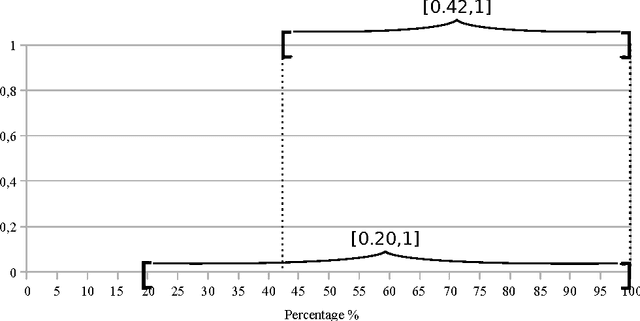
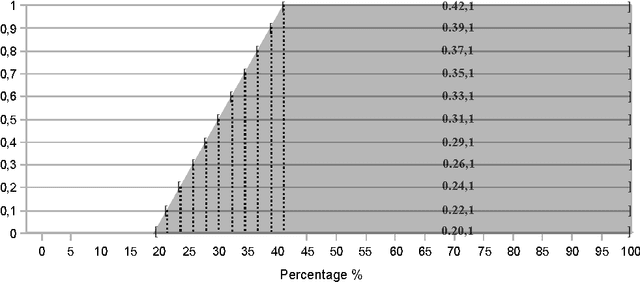
In this paper, a new approximate syllogistic reasoning schema is described that expands some of the approaches expounded in the literature into two ways: (i) a number of different types of quantifiers (logical, absolute, proportional, comparative and exception) taken from Theory of Generalized Quantifiers and similarity quantifiers, taken from statistics, are considered and (ii) any number of premises can be taken into account within the reasoning process. Furthermore, a systematic reasoning procedure to solve the syllogism is also proposed, interpreting it as an equivalent mathematical optimization problem, where the premises constitute the constraints of the searching space for the quantifier in the conclusion.

Some Reflections on the Set-based and the Conditional-based Interpretations of Statements in Syllogistic Reasoning

Two interpretations about syllogistic statements are described in this paper. One is the so-called set-based interpretation, which assumes that quantified statements and syllogisms talk about quantity-relationships between sets. The other one, the so-called conditional interpretation, assumes that quantified propositions talk about conditional propositions and how strong are the links between the antecedent and the consequent. Both interpretations are compared attending to three different questions (existential import, singular statements and non-proportional quantifiers) from the point of view of their impact on the further development of this type of reasoning.