On the analysis of set-based fuzzy quantified reasoning using classical syllogistics
Paper and Code
Nov 27, 2014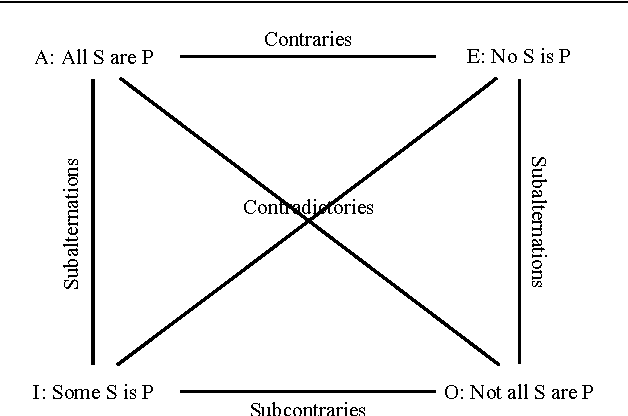
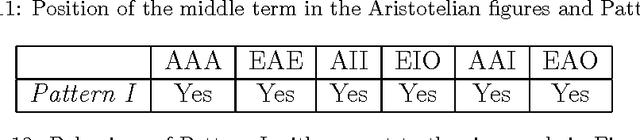
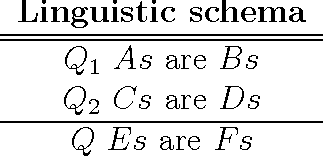
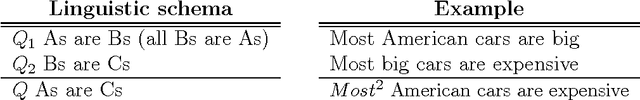
Syllogism is a type of deductive reasoning involving quantified statements. The syllogistic reasoning scheme in the classical Aristotelian framework involves three crisp term sets and four linguistic quantifiers, for which the main support is the linguistic properties of the quantifiers. A number of fuzzy approaches for defining an approximate syllogism have been proposed for which the main support is cardinality calculus. In this paper we analyze fuzzy syllogistic models previously described by Zadeh and Dubois et al. and compare their behavior with that of the classical Aristotelian framework to check which of the 24 classical valid syllogistic reasoning patterns or moods are particular crisp cases of these fuzzy approaches. This allows us to assess to what extent these approaches can be considered as either plausible extensions of the classical crisp syllogism or a basis for a general approach to the problem of approximate syllogism.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge