Fuzzy quantification for linguistic data analysis and data mining

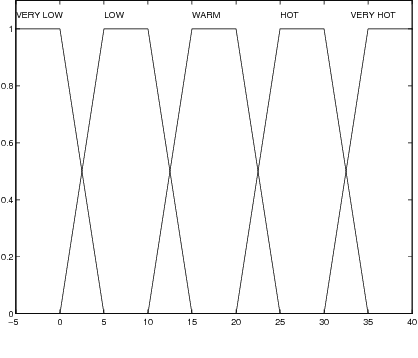
Fuzzy quantification is a subtopic of fuzzy logic which deals with the modelling of the quantified expressions we can find in natural language. Fuzzy quantifiers have been successfully applied in several fields like fuzzy, control, fuzzy databases, information retrieval, natural language generation, etc. Their ability to model and evaluate linguistic expressions in a mathematical way, makes fuzzy quantifiers very powerful for data analytics and data mining applications. In this paper we will give a general overview of the main applications of fuzzy quantifiers in this field as well as some ideas to use them in new application contexts.

On the analysis of set-based fuzzy quantified reasoning using classical syllogistics

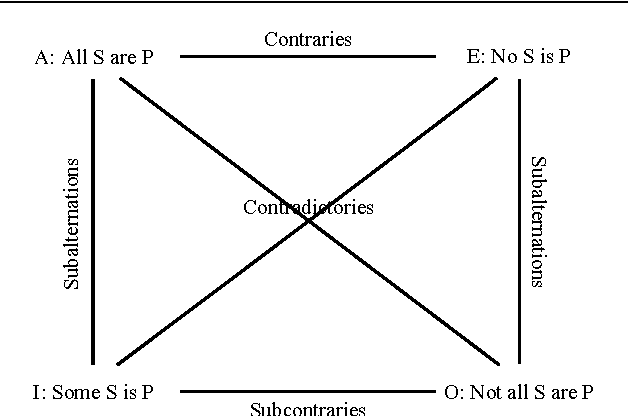
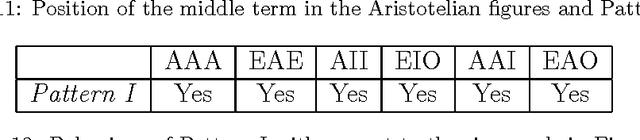
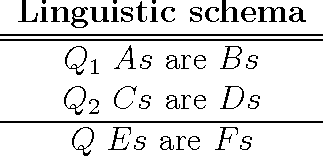
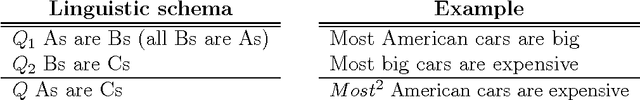
Syllogism is a type of deductive reasoning involving quantified statements. The syllogistic reasoning scheme in the classical Aristotelian framework involves three crisp term sets and four linguistic quantifiers, for which the main support is the linguistic properties of the quantifiers. A number of fuzzy approaches for defining an approximate syllogism have been proposed for which the main support is cardinality calculus. In this paper we analyze fuzzy syllogistic models previously described by Zadeh and Dubois et al. and compare their behavior with that of the classical Aristotelian framework to check which of the 24 classical valid syllogistic reasoning patterns or moods are particular crisp cases of these fuzzy approaches. This allows us to assess to what extent these approaches can be considered as either plausible extensions of the classical crisp syllogism or a basis for a general approach to the problem of approximate syllogism.

A Fuzzy Syllogistic Reasoning Schema for Generalized Quantifiers

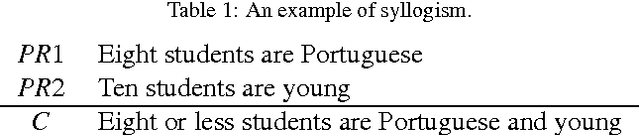
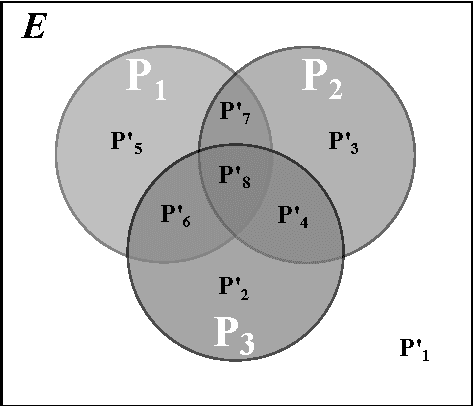
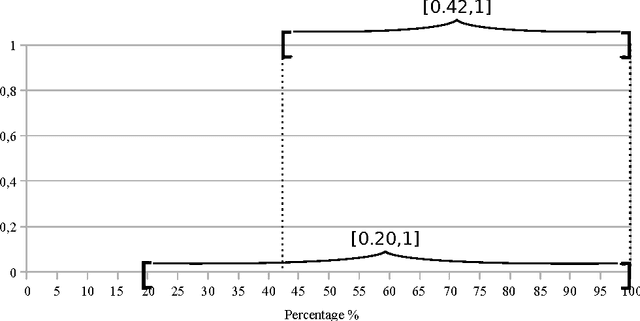
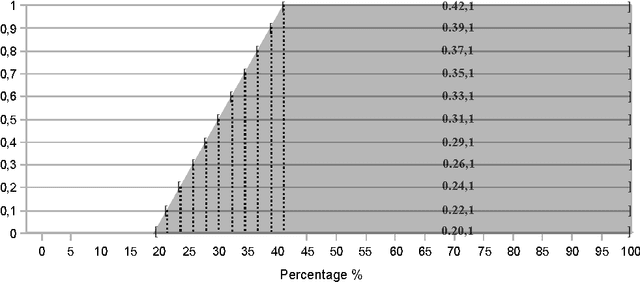
In this paper, a new approximate syllogistic reasoning schema is described that expands some of the approaches expounded in the literature into two ways: (i) a number of different types of quantifiers (logical, absolute, proportional, comparative and exception) taken from Theory of Generalized Quantifiers and similarity quantifiers, taken from statistics, are considered and (ii) any number of premises can be taken into account within the reasoning process. Furthermore, a systematic reasoning procedure to solve the syllogism is also proposed, interpreting it as an equivalent mathematical optimization problem, where the premises constitute the constraints of the searching space for the quantifier in the conclusion.