Smart Vision-Language Reasoners

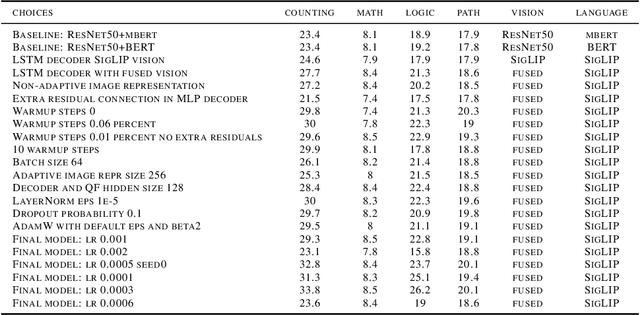
In this article, we investigate vision-language models (VLM) as reasoners. The ability to form abstractions underlies mathematical reasoning, problem-solving, and other Math AI tasks. Several formalisms have been given to these underlying abstractions and skills utilized by humans and intelligent systems for reasoning. Furthermore, human reasoning is inherently multimodal, and as such, we focus our investigations on multimodal AI. In this article, we employ the abstractions given in the SMART task (Simple Multimodal Algorithmic Reasoning Task) introduced in \cite{cherian2022deep} as meta-reasoning and problem-solving skills along eight axes: math, counting, path, measure, logic, spatial, and pattern. We investigate the ability of vision-language models to reason along these axes and seek avenues of improvement. Including composite representations with vision-language cross-attention enabled learning multimodal representations adaptively from fused frozen pretrained backbones for better visual grounding. Furthermore, proper hyperparameter and other training choices led to strong improvements (up to $48\%$ gain in accuracy) on the SMART task, further underscoring the power of deep multimodal learning. The smartest VLM, which includes a novel QF multimodal layer, improves upon the best previous baselines in every one of the eight fundamental reasoning skills. End-to-end code is available at https://github.com/smarter-vlm/smarter.

An Expectation Maximization Framework for Yule-Simon Preferential Attachment Models

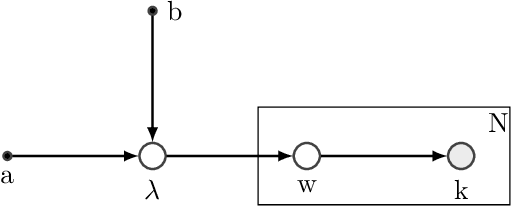
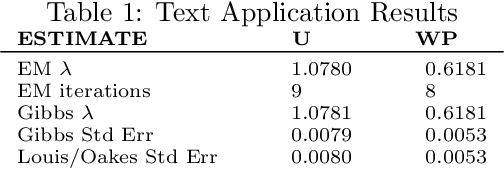
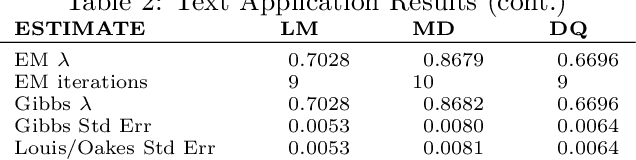
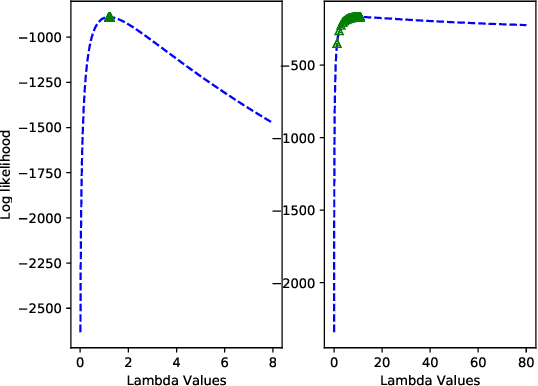
In this paper we develop an Expectation Maximization(EM) algorithm to estimate the parameter of a Yule-Simon distribution. The Yule-Simon distribution exhibits the "rich get richer" effect whereby an 80-20 type of rule tends to dominate. These distributions are ubiquitous in industrial settings. The EM algorithm presented provides both frequentist and Bayesian estimates of the $\lambda$ parameter. By placing the estimation method within the EM framework we are able to derive Standard errors of the resulting estimate. Additionally, we prove convergence of the Yule-Simon EM algorithm and study the rate of convergence. An explicit, closed form solution for the rate of convergence of the algorithm is given.

Gini-regularized Optimal Transport with an Application to Spatio-Temporal Forecasting

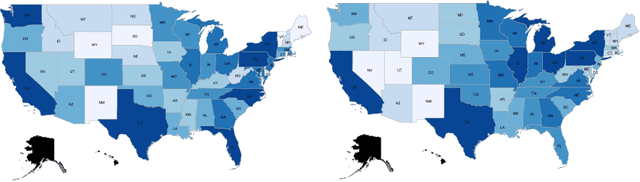
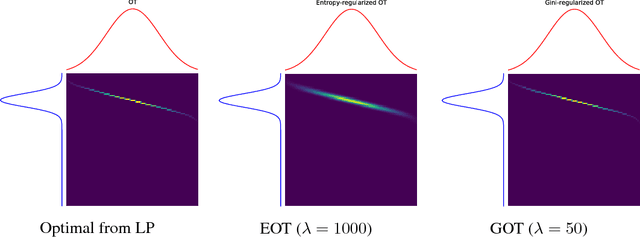
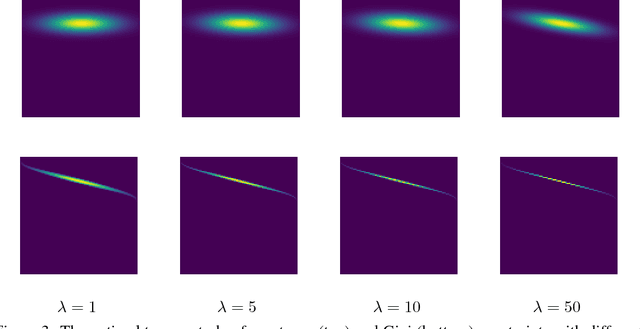
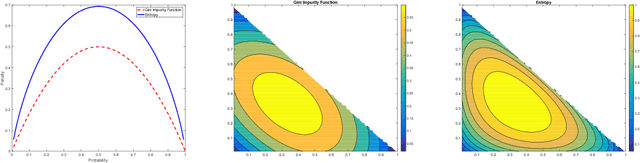
Rapidly growing product lines and services require a finer-granularity forecast that considers geographic locales. However the open question remains, how to assess the quality of a spatio-temporal forecast? In this manuscript we introduce a metric to evaluate spatio-temporal forecasts. This metric is based on an Opti- mal Transport (OT) problem. The metric we propose is a constrained OT objec- tive function using the Gini impurity function as a regularizer. We demonstrate through computer experiments both the qualitative and the quantitative charac- teristics of the Gini regularized OT problem. Moreover, we show that the Gini regularized OT problem converges to the classical OT problem, when the Gini regularized problem is considered as a function of {\lambda}, the regularization parame-ter. The convergence to the classical OT solution is faster than the state-of-the-art Entropic-regularized OT[Cuturi, 2013] and results in a numerically more stable algorithm.