Gini-regularized Optimal Transport with an Application to Spatio-Temporal Forecasting
Paper and Code
Dec 07, 2017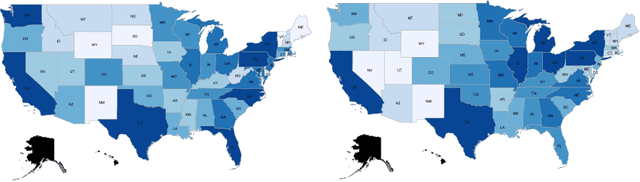
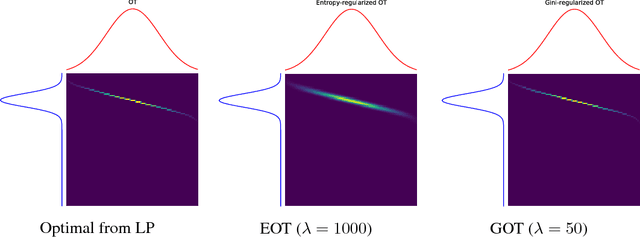
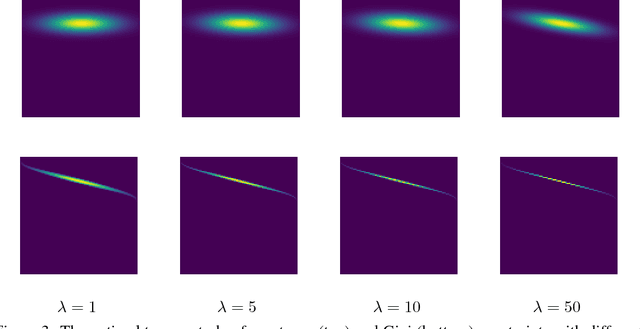
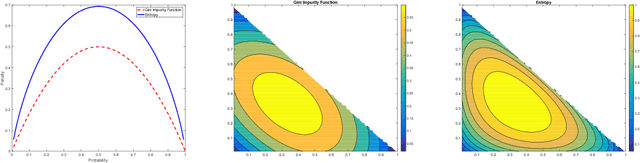
Rapidly growing product lines and services require a finer-granularity forecast that considers geographic locales. However the open question remains, how to assess the quality of a spatio-temporal forecast? In this manuscript we introduce a metric to evaluate spatio-temporal forecasts. This metric is based on an Opti- mal Transport (OT) problem. The metric we propose is a constrained OT objec- tive function using the Gini impurity function as a regularizer. We demonstrate through computer experiments both the qualitative and the quantitative charac- teristics of the Gini regularized OT problem. Moreover, we show that the Gini regularized OT problem converges to the classical OT problem, when the Gini regularized problem is considered as a function of {\lambda}, the regularization parame-ter. The convergence to the classical OT solution is faster than the state-of-the-art Entropic-regularized OT[Cuturi, 2013] and results in a numerically more stable algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge