An Expectation Maximization Framework for Yule-Simon Preferential Attachment Models

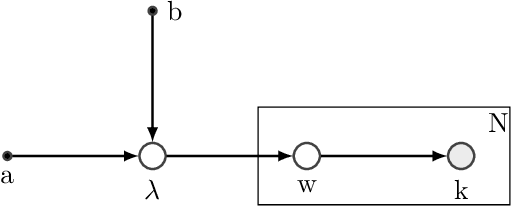
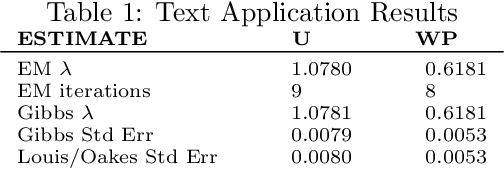
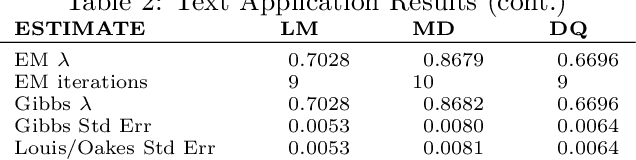
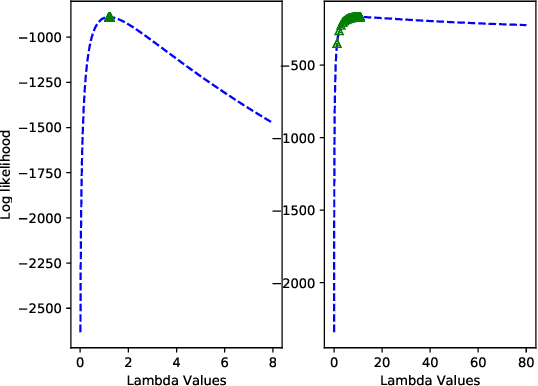
In this paper we develop an Expectation Maximization(EM) algorithm to estimate the parameter of a Yule-Simon distribution. The Yule-Simon distribution exhibits the "rich get richer" effect whereby an 80-20 type of rule tends to dominate. These distributions are ubiquitous in industrial settings. The EM algorithm presented provides both frequentist and Bayesian estimates of the $\lambda$ parameter. By placing the estimation method within the EM framework we are able to derive Standard errors of the resulting estimate. Additionally, we prove convergence of the Yule-Simon EM algorithm and study the rate of convergence. An explicit, closed form solution for the rate of convergence of the algorithm is given.