Global Simulation-Guided Dynamic Operator Scheduling for Efficient Multi-Tenant Model Serving

Container-granularity scheduling leaves abundant short-lived idle slices within containers unexploited. Reallocating containers is too heavyweight to utilize such fine-grained opportunities under SLA constraints, and operator-level scheduling requires reasoning about dependencies, memory safety, and cluster-wide execution dynamics in real time. In this paper, we present SliceScheduler, a dynamic operator-level scheduling system for multi-tenant model serving. The key idea is to expose cluster-wide operator execution state and enable what-if reasoning over scheduling decisions. SliceScheduler consists of four key components. First, we introduce the Global Mapping Graph (GMG), a unified abstraction that captures operator dependencies, tensor shapes, resource mappings, and execution states, providing a real-time, cluster-wide view with explicit resource semantics. Second, we build a global simulator on top of GMG to predict operator-level execution and memory evolution under candidate placements. Third, we design an incremental, simulation-based scheduling module that selects placements to exploit fragmented idle slices while avoiding memory violations and preserving SLA. Finally, we develop an operator executor that materializes scheduling decisions on GPUs and coordinates computation and cross-accelerator transfers. We implement SliceScheduler as a PyTorch backend and evaluate it using production trace replay. Experimental results show that SliceScheduler improves token throughput by 1.10--2.29$\times$ compared to existing approaches, while maintaining SLA violations within 9\%. SliceScheduler demonstrates that operator-level scheduling is a practical and effective approach to improving GPU utilization for multi-tenant LLM serving.

Covariate-guided Bayesian mixture model for multivariate time series

With rapid development of techniques to measure brain activity and structure, statistical methods for analyzing modern brain-imaging play an important role in the advancement of science. Imaging data that measure brain function are usually multivariate time series and are heterogeneous across both imaging sources and subjects, which lead to various statistical and computational challenges. In this paper, we propose a group-based method to cluster a collection of multivariate time series via a Bayesian mixture of smoothing splines. Our method assumes each multivariate time series is a mixture of multiple components with different mixing weights. Time-independent covariates are assumed to be associated with the mixture components and are incorporated via logistic weights of a mixture-of-experts model. We formulate this approach under a fully Bayesian framework using Gibbs sampling where the number of components is selected based on a deviance information criterion. The proposed method is compared to existing methods via simulation studies and is applied to a study on functional near-infrared spectroscopy (fNIRS), which aims to understand infant emotional reactivity and recovery from stress. The results reveal distinct patterns of brain activity, as well as associations between these patterns and selected covariates.

RISE: Robust Individualized Decision Learning with Sensitive Variables

This paper introduces RISE, a robust individualized decision learning framework with sensitive variables, where sensitive variables are collectible data and important to the intervention decision, but their inclusion in decision making is prohibited due to reasons such as delayed availability or fairness concerns. A naive baseline is to ignore these sensitive variables in learning decision rules, leading to significant uncertainty and bias. To address this, we propose a decision learning framework to incorporate sensitive variables during offline training but not include them in the input of the learned decision rule during model deployment. Specifically, from a causal perspective, the proposed framework intends to improve the worst-case outcomes of individuals caused by sensitive variables that are unavailable at the time of decision. Unlike most existing literature that uses mean-optimal objectives, we propose a robust learning framework by finding a newly defined quantile- or infimum-optimal decision rule. The reliable performance of the proposed method is demonstrated through synthetic experiments and three real-world applications.

A Tree-based Federated Learning Approach for Personalized Treatment Effect Estimation from Heterogeneous Data Sources

Federated learning is an appealing framework for analyzing sensitive data from distributed health data networks due to its protection of data privacy. Under this framework, data partners at local sites collaboratively build an analytical model under the orchestration of a coordinating site, while keeping the data decentralized. However, existing federated learning methods mainly assume data across sites are homogeneous samples of the global population, hence failing to properly account for the extra variability across sites in estimation and inference. Drawing on a multi-hospital electronic health records network, we develop an efficient and interpretable tree-based ensemble of personalized treatment effect estimators to join results across hospital sites, while actively modeling for the heterogeneity in data sources through site partitioning. The efficiency of our method is demonstrated by a study of causal effects of oxygen saturation on hospital mortality and backed up by comprehensive numerical results.

A sparse negative binomial mixture model for clustering RNA-seq count data

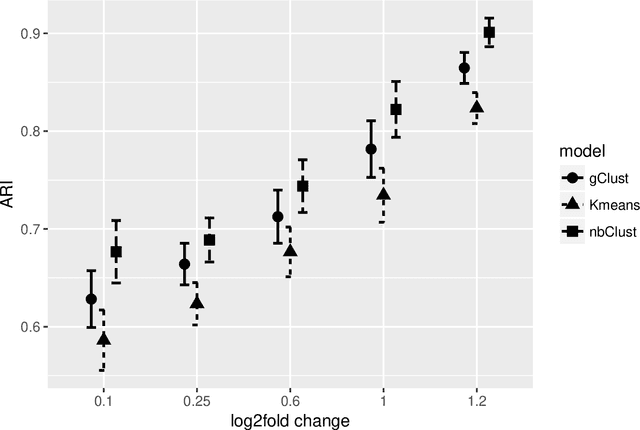
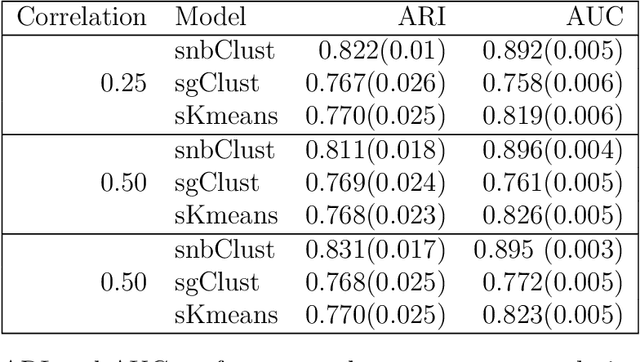
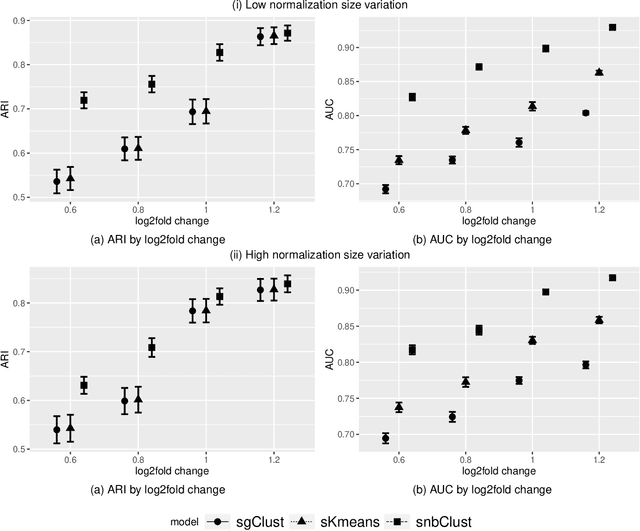
Clustering with variable selection is a challenging but critical task for modern small-n-large-p data. Existing methods based on Gaussian mixture models or sparse K-means provide solutions to continuous data. With the prevalence of RNA-seq technology and lack of count data modeling for clustering, the current practice is to normalize count expression data into continuous measures and apply existing models with Gaussian assumption. In this paper, we develop a negative binomial mixture model with gene regularization to cluster samples (small $n$) with high-dimensional gene features (large $p$). EM algorithm and Bayesian information criterion are used for inference and determining tuning parameters. The method is compared with sparse Gaussian mixture model and sparse K-means using extensive simulations and two real transcriptomic applications in breast cancer and rat brain studies. The result shows superior performance of the proposed count data model in clustering accuracy, feature selection and biological interpretation by pathway enrichment analysis.

Method of Contraction-Expansion (MOCE) for Simultaneous Inference in Linear Models

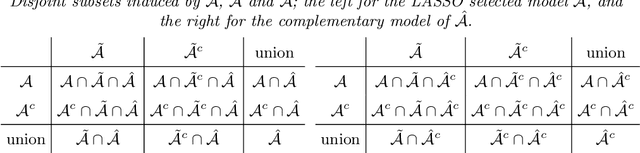
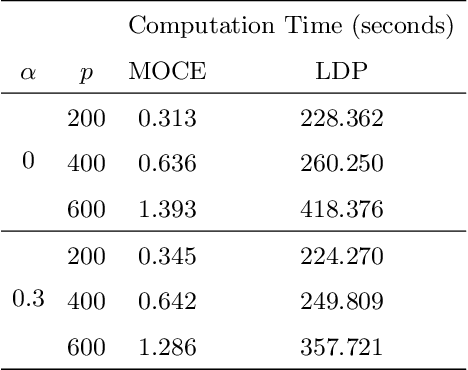
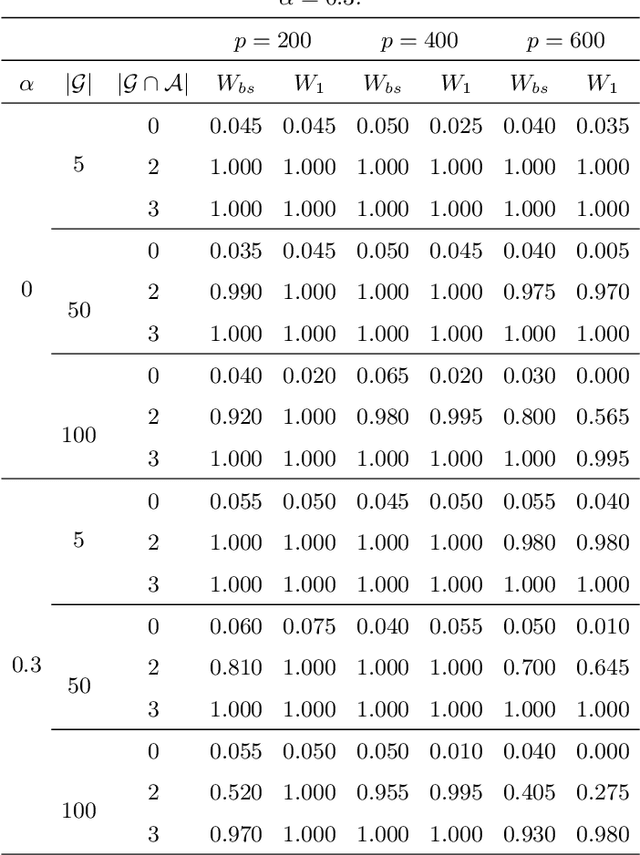
Simultaneous inference after model selection is of critical importance to address scientific hypotheses involving a set of parameters. In this paper, we consider high-dimensional linear regression model in which a regularization procedure such as LASSO is applied to yield a sparse model. To establish a simultaneous post-model selection inference, we propose a method of contraction and expansion (MOCE) along the line of debiasing estimation that enables us to balance the bias-and-variance trade-off so that the super-sparsity assumption may be relaxed. We establish key theoretical results for the proposed MOCE procedure from which the expanded model can be selected with theoretical guarantees and simultaneous confidence regions can be constructed by the joint asymptotic normal distribution. In comparison with existing methods, our proposed method exhibits stable and reliable coverage at a nominal significance level with substantially less computational burden, and thus it is trustworthy for its application in solving real-world problems.