Peter X. -K. Song
Supervised Homogeneity Fusion: a Combinatorial Approach
Jan 04, 2022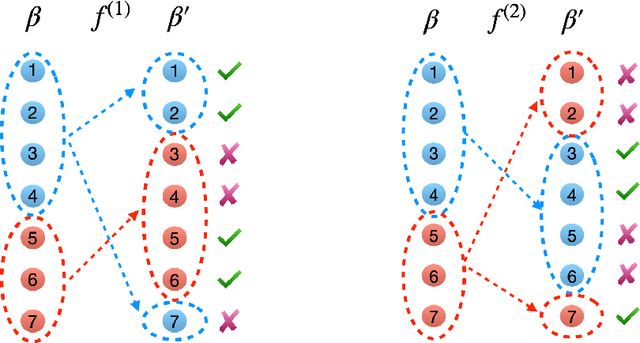
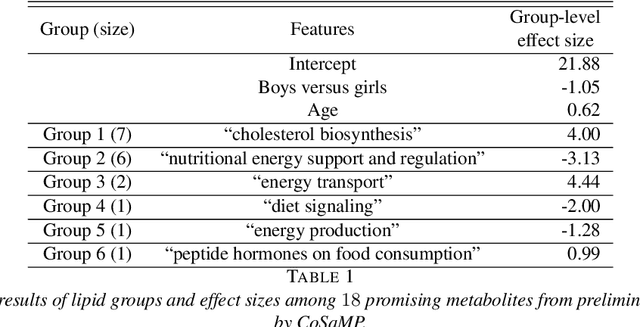
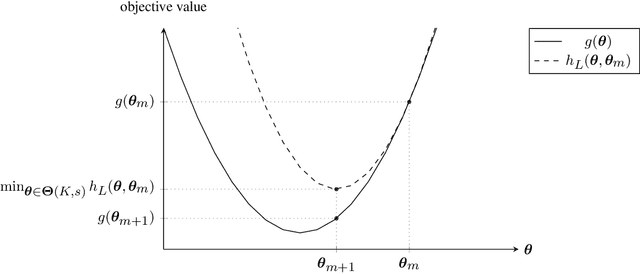
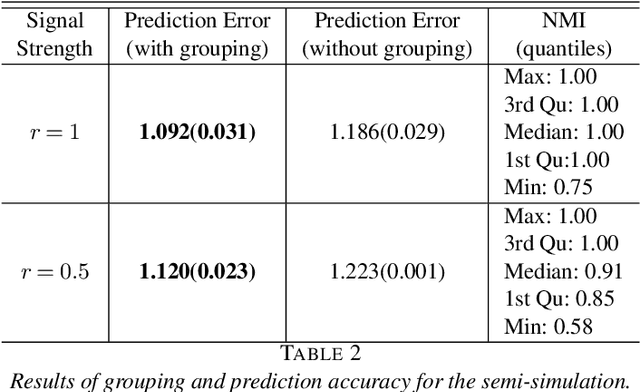
Abstract:Fusing regression coefficients into homogenous groups can unveil those coefficients that share a common value within each group. Such groupwise homogeneity reduces the intrinsic dimension of the parameter space and unleashes sharper statistical accuracy. We propose and investigate a new combinatorial grouping approach called $L_0$-Fusion that is amenable to mixed integer optimization (MIO). On the statistical aspect, we identify a fundamental quantity called grouping sensitivity that underpins the difficulty of recovering the true groups. We show that $L_0$-Fusion achieves grouping consistency under the weakest possible requirement of the grouping sensitivity: if this requirement is violated, then the minimax risk of group misspecification will fail to converge to zero. Moreover, we show that in the high-dimensional regime, one can apply $L_0$-Fusion coupled with a sure screening set of features without any essential loss of statistical efficiency, while reducing the computational cost substantially. On the algorithmic aspect, we provide a MIO formulation for $L_0$-Fusion along with a warm start strategy. Simulation and real data analysis demonstrate that $L_0$-Fusion exhibits superiority over its competitors in terms of grouping accuracy.
Method of Contraction-Expansion (MOCE) for Simultaneous Inference in Linear Models
Aug 04, 2019
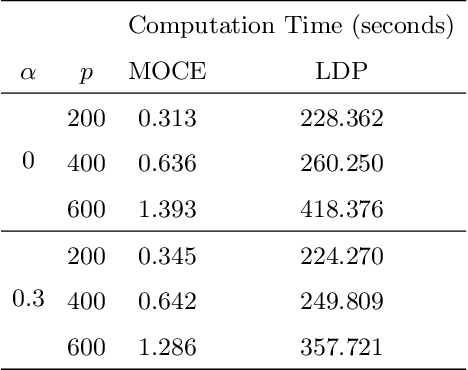
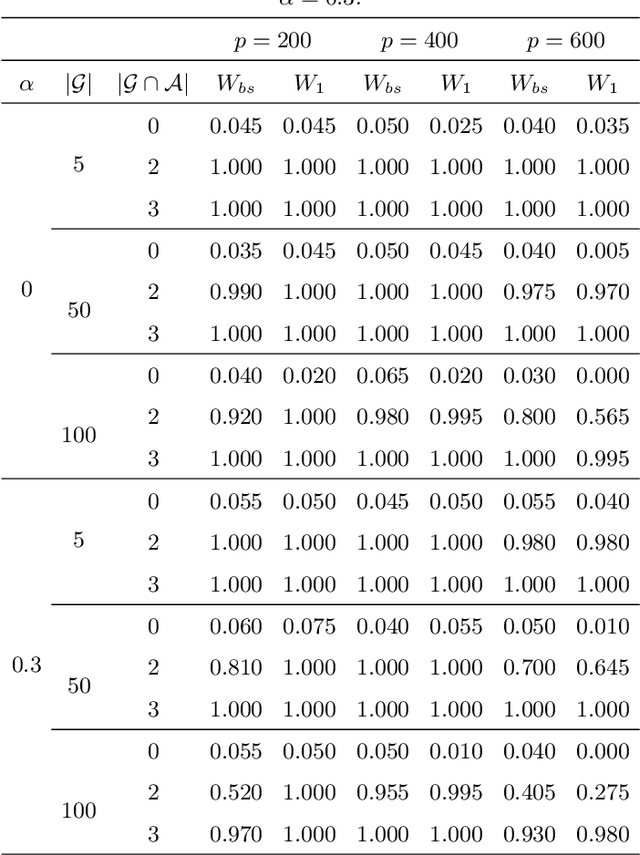
Abstract:Simultaneous inference after model selection is of critical importance to address scientific hypotheses involving a set of parameters. In this paper, we consider high-dimensional linear regression model in which a regularization procedure such as LASSO is applied to yield a sparse model. To establish a simultaneous post-model selection inference, we propose a method of contraction and expansion (MOCE) along the line of debiasing estimation that enables us to balance the bias-and-variance trade-off so that the super-sparsity assumption may be relaxed. We establish key theoretical results for the proposed MOCE procedure from which the expanded model can be selected with theoretical guarantees and simultaneous confidence regions can be constructed by the joint asymptotic normal distribution. In comparison with existing methods, our proposed method exhibits stable and reliable coverage at a nominal significance level with substantially less computational burden, and thus it is trustworthy for its application in solving real-world problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge