Supervised Homogeneity Fusion: a Combinatorial Approach
Paper and Code
Jan 04, 2022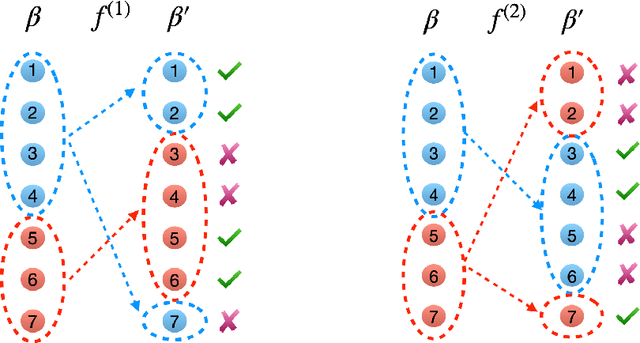
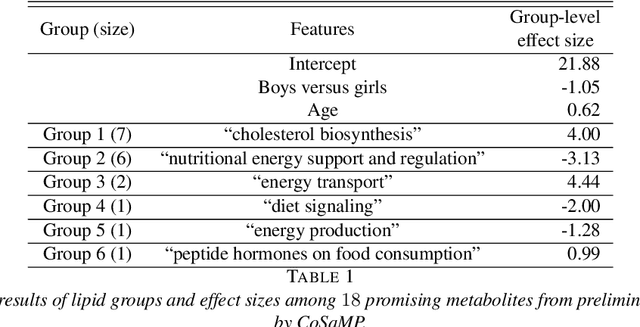
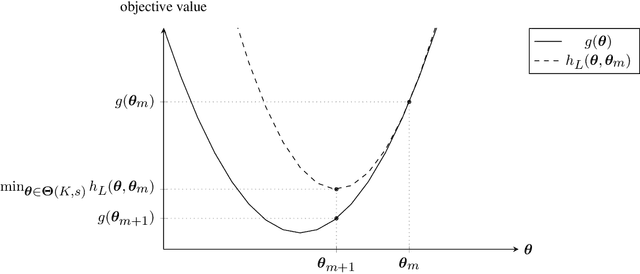
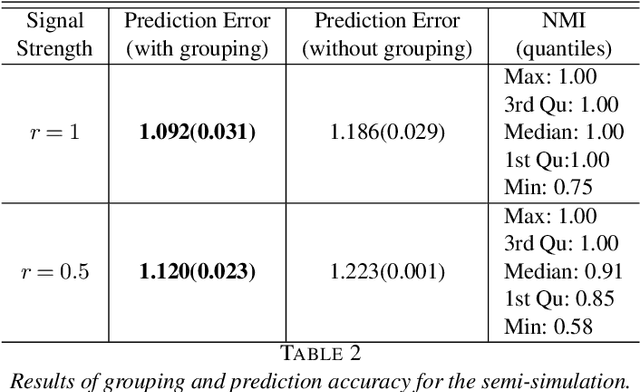
Fusing regression coefficients into homogenous groups can unveil those coefficients that share a common value within each group. Such groupwise homogeneity reduces the intrinsic dimension of the parameter space and unleashes sharper statistical accuracy. We propose and investigate a new combinatorial grouping approach called $L_0$-Fusion that is amenable to mixed integer optimization (MIO). On the statistical aspect, we identify a fundamental quantity called grouping sensitivity that underpins the difficulty of recovering the true groups. We show that $L_0$-Fusion achieves grouping consistency under the weakest possible requirement of the grouping sensitivity: if this requirement is violated, then the minimax risk of group misspecification will fail to converge to zero. Moreover, we show that in the high-dimensional regime, one can apply $L_0$-Fusion coupled with a sure screening set of features without any essential loss of statistical efficiency, while reducing the computational cost substantially. On the algorithmic aspect, we provide a MIO formulation for $L_0$-Fusion along with a warm start strategy. Simulation and real data analysis demonstrate that $L_0$-Fusion exhibits superiority over its competitors in terms of grouping accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge