SMPL-IK: Learned Morphology-Aware Inverse Kinematics for AI Driven Artistic Workflows

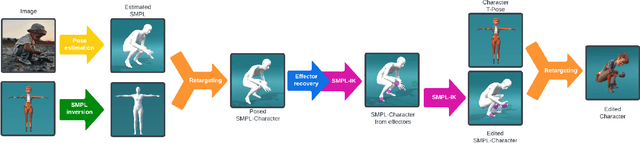
Inverse Kinematics (IK) systems are often rigid with respect to their input character, thus requiring user intervention to be adapted to new skeletons. In this paper we aim at creating a flexible, learned IK solver applicable to a wide variety of human morphologies. We extend a state-of-the-art machine learning IK solver to operate on the well known Skinned Multi-Person Linear model (SMPL). We call our model SMPL-IK, and show that when integrated into real-time 3D software, this extended system opens up opportunities for defining novel AI-assisted animation workflows. For example, pose authoring can be made more flexible with SMPL-IK by allowing users to modify gender and body shape while posing a character. Additionally, when chained with existing pose estimation algorithms, SMPL-IK accelerates posing by allowing users to bootstrap 3D scenes from 2D images while allowing for further editing. Finally, we propose a novel SMPL Shape Inversion mechanism (SMPL-SI) to map arbitrary humanoid characters to the SMPL space, allowing artists to leverage SMPL-IK on custom characters. In addition to qualitative demos showing proposed tools, we present quantitative SMPL-IK baselines on the H36M and AMASS datasets.

Motion Inbetweening via Deep $Δ$-Interpolator

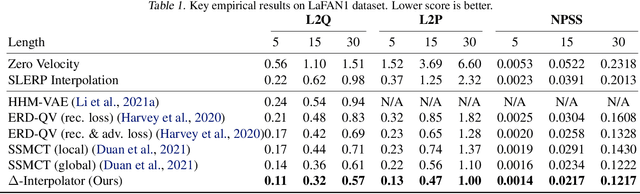
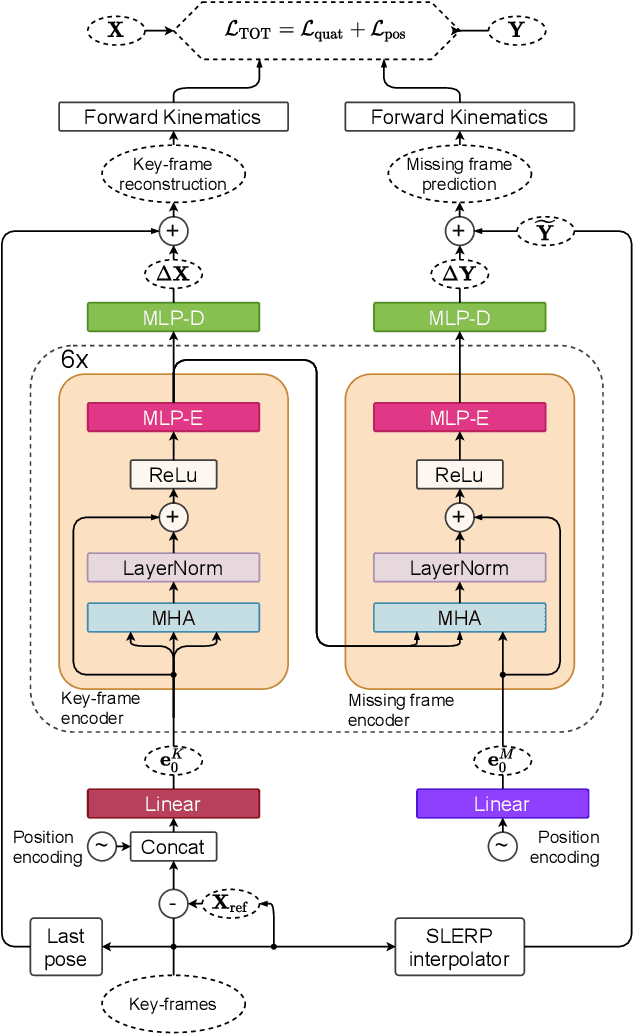
We show that the task of synthesizing missing middle frames, commonly known as motion in-betweening in the animation industry, can be solved more accurately and effectively if a deep learning interpolator operates in the delta mode, using the spherical linear interpolator as a baseline. We demonstrate our empirical findings on the publicly available LaFAN1 dataset. We further generalize this result by showing that the $\Delta$-regime is viable with respect to the reference of the last known frame (also known as the zero-velocity model). This supports the more general conclusion that deep in-betweening in the reference frame local to input frames is more accurate and robust than in-betweening in the global (world) reference frame advocated in previous work. Our code is publicly available at https://github.com/boreshkinai/delta-interpolator.