Linear-time calculation of the expected sum of edge lengths in planar linearizations of trees

Dependency graphs have proven to be a very successful model to represent the syntactic structure of sentences of human languages. In these graphs, widely accepted to be trees, vertices are words and arcs connect syntactically-dependent words. The tendency of these dependencies to be short has been demonstrated using random baselines for the sum of the lengths of the edges or its variants. A ubiquitous baseline is the expected sum in projective orderings (wherein edges do not cross and the root word of the sentence is not covered by any edge). It was shown that said expected value can be computed in $O(n)$ time. In this article we focus on planar orderings (where the root word can be covered) and present two main results. First, we show the relationship between the expected sum in planar arrangements and the expected sum in projective arrangements. Second, we also derive a $O(n)$-time algorithm to calculate the expected value of the sum of edge lengths. These two results stem from another contribution of the present article, namely a characterization of planarity that, given a sentence, yields either the number of planar permutations or an efficient algorithm to generate uniformly random planar permutations of the words. Our research paves the way for replicating past research on dependency distance minimization using random planar linearizations as random baseline.

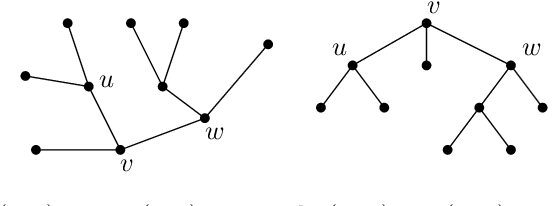
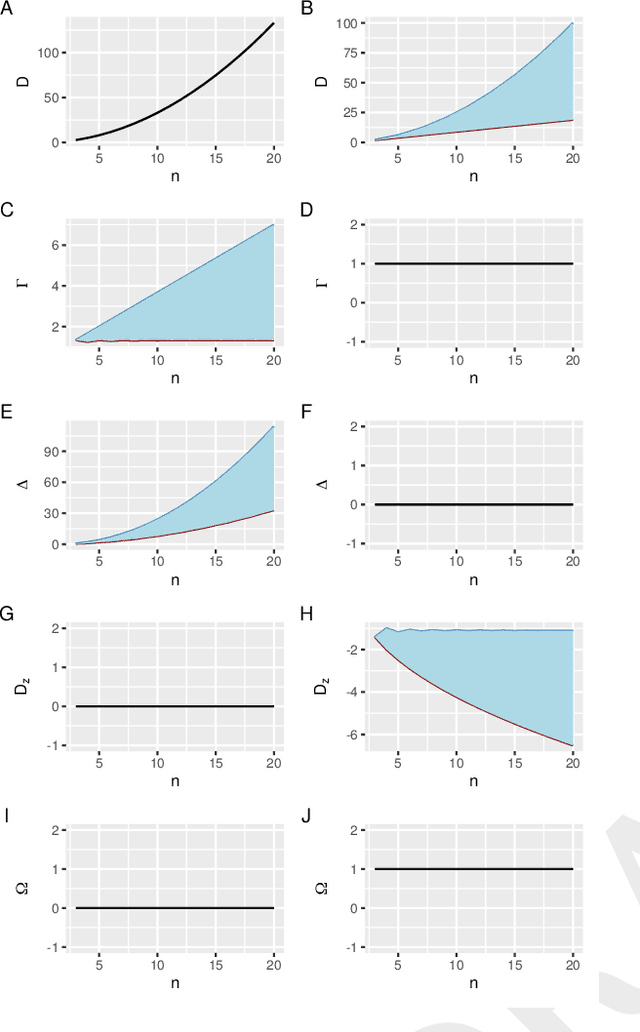
The Maximum Linear Arrangement Problem for trees under projectivity and planarity

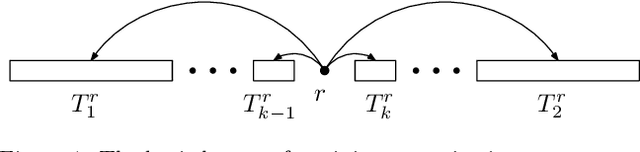
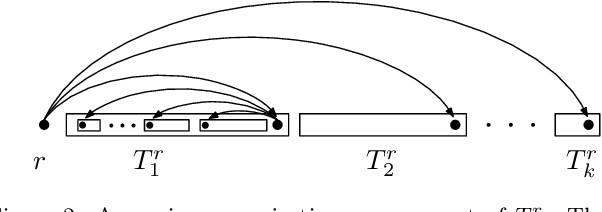
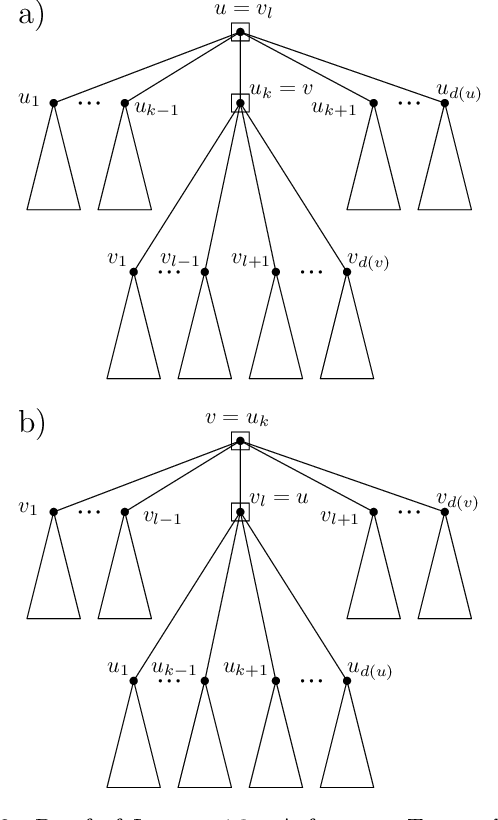
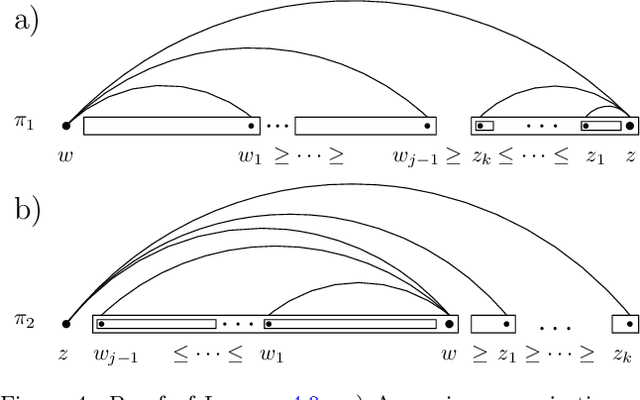
The Maximum Linear Arrangement problem (MaxLA) consists of finding a mapping $\pi$ from the $n$ vertices of a graph $G$ to distinct consecutive integers that maximizes $D_{\pi}(G)=\sum_{uv\in E(G)}|\pi(u) - \pi(v)|$. In this setting, vertices are considered to lie on a horizontal line and edges are drawn as semicircles above the line. There exist variants of MaxLA in which the arrangements are constrained. In the planar variant edge crossings are forbidden. In the projective variant for rooted trees arrangements are planar and the root cannot be covered by any edge. Here we present $O(n)$-time and $O(n)$-space algorithms that solve Planar and Projective MaxLA for trees. We also prove several properties of maximum projective and planar arrangements.

The Linear Arrangement Library. A new tool for research on syntactic dependency structures

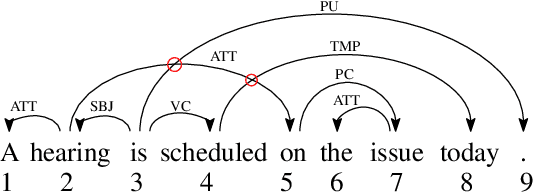
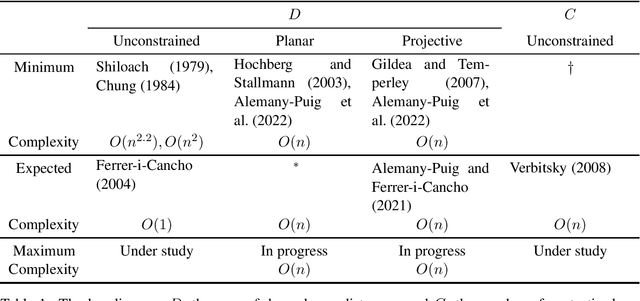
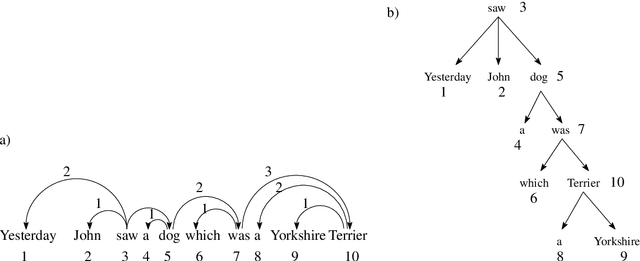
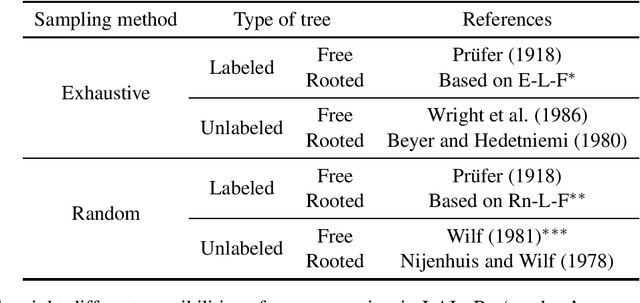
The new and growing field of Quantitative Dependency Syntax has emerged at the crossroads between Dependency Syntax and Quantitative Linguistics. One of the main concerns in this field is the statistical patterns of syntactic dependency structures. These structures, grouped in treebanks, are the source for statistical analyses in these and related areas; dozens of scores devised over the years are the tools of a new industry to search for patterns and perform other sorts of analyses. The plethora of such metrics and their increasing complexity require sharing the source code of the programs used to perform such analyses. However, such code is not often shared with the scientific community or is tested following unknown standards. Here we present a new open-source tool, the Linear Arrangement Library (LAL), which caters to the needs of, especially, inexperienced programmers. This tool enables the calculation of these metrics on single syntactic dependency structures, treebanks, and collection of treebanks, grounded on ease of use and yet with great flexibility. LAL has been designed to be efficient, easy to use (while satisfying the needs of all levels of programming expertise), reliable (thanks to thorough testing), and to unite research from different traditions, geographic areas, and research fields.

Linear-time calculation of the expected sum of edge lengths in random projective linearizations of trees

The syntactic structure of a sentence is often represented using syntactic dependency trees. The sum of the distances between syntactically related words has been in the limelight for the past decades. Research on dependency distances led to the formulation of the principle of dependency distance minimization whereby words in sentences are ordered so as to minimize that sum. Numerous random baselines have been defined to carry out related quantitative studies on languages. The simplest random baseline is the expected value of the sum in unconstrained random permutations of the words in the sentence, namely when all the shufflings of the words of a sentence are allowed and equally likely. Here we focus on a popular baseline: random projective permutations of the words of the sentence, that is, permutations where the syntactic dependency structure is projective, a formal constraint that sentences satisfy often in languages. Thus far, the expectation of the sum of dependency distances in random projective shufflings of a sentence has been estimated approximately with a Monte Carlo procedure whose cost is of the order of $Zn$, where $n$ is the number of words of the sentence and $Z$ is the number of samples; the larger $Z$, the lower the error of the estimation but the larger the time cost. Here we present formulae to compute that expectation without error in time of the order of $n$. Furthermore, we show that star trees maximize it, and devise a dynamic programming algorithm to retrieve the trees that minimize it.

Minimum projective linearizations of trees in linear time

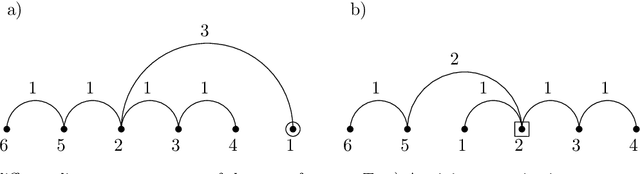
The minimum linear arrangement problem (MLA) consists of finding a mapping $\pi$ from vertices of a graph to integers that minimizes $\sum_{uv\in E}|\pi(u) - \pi(v)|$. For trees, various algorithms are available to solve the problem in polynomial time; the best known runs in subquadratic time in $n=|V|$. There exist variants of the MLA in which the arrangements are constrained to certain classes of projectivity. Iordanskii, and later Hochberg and Stallmann (HS), put forward $O(n)$-time algorithms that solve the problem when arrangements are constrained to be planar. We also consider linear arrangements of rooted trees that are constrained to be projective. Gildea and Temperley (GT) sketched an algorithm for the projectivity constraint which, as they claimed, runs in $O(n)$ but did not provide any justification of its cost. In contrast, Park and Levy claimed that GT's algorithm runs in $O(n \log d_{max})$ where $d_{max}$ is the maximum degree but did not provide sufficient detail. Here we correct an error in HS's algorithm for the planar case, show its relationship with the projective case, and derive an algorithm for the projective case that runs undoubtlessly in $O(n)$-time.

The optimality of syntactic dependency distances

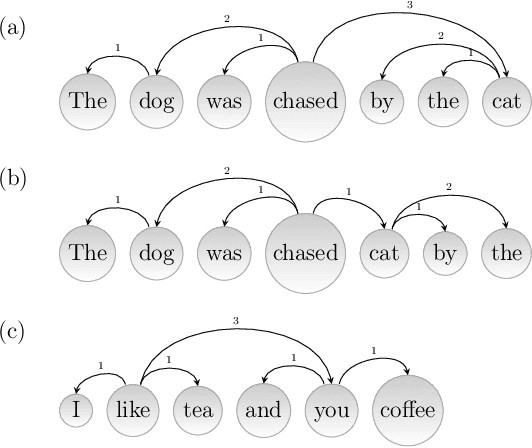
It is often stated that human languages, as other biological systems, are shaped by cost-cutting pressures but, to what extent? Attempts to quantify the degree of optimality of languages by means of an optimality score have been scarce and focused mostly on English. Here we recast the problem of the optimality of the word order of a sentence as an optimization problem on a spatial network where the vertices are words, arcs indicate syntactic dependencies and the space is defined by the linear order of the words in the sentence. We introduce a new score to quantify the cognitive pressure to reduce the distance between linked words in a sentence. The analysis of sentences from 93 languages representing 19 linguistic families reveals that half of languages are optimized to a 70% or more. The score indicates that distances are not significantly reduced in a few languages and confirms two theoretical predictions, i.e. that longer sentences are more optimized and that distances are more likely to be longer than expected by chance in short sentences. We present a new hierarchical ranking of languages by their degree of optimization. The statistical advantages of the new score call for a reevaluation of the evolution of dependency distance over time in languages as well as the relationship between dependency distance and linguistic competence. Finally, the principles behind the design of the score can be extended to develop more powerful normalizations of topological distances or physical distances in more dimensions.