The Maximum Linear Arrangement Problem for trees under projectivity and planarity
Paper and Code
Jun 16, 2022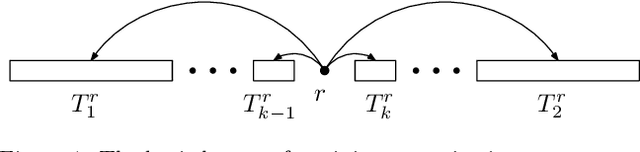
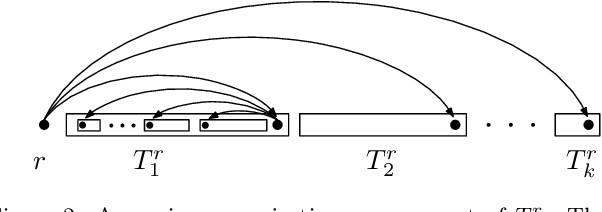
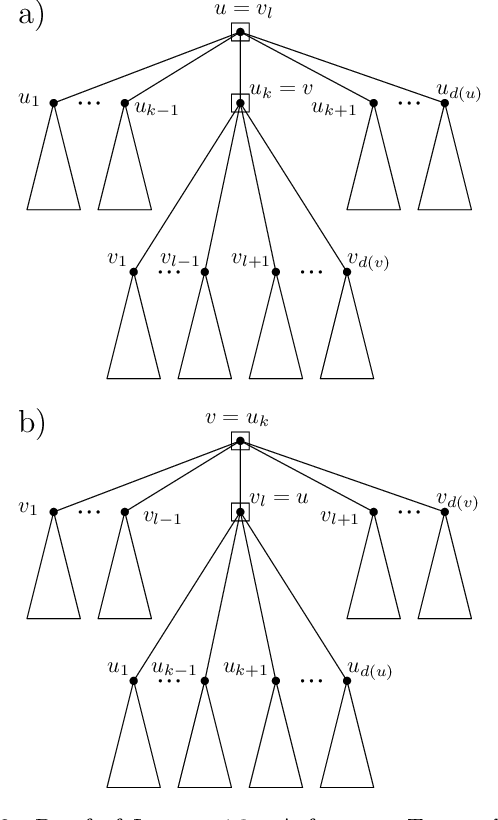
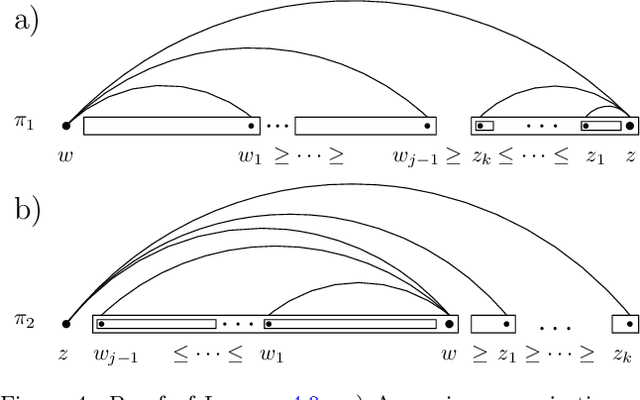
The Maximum Linear Arrangement problem (MaxLA) consists of finding a mapping $\pi$ from the $n$ vertices of a graph $G$ to distinct consecutive integers that maximizes $D_{\pi}(G)=\sum_{uv\in E(G)}|\pi(u) - \pi(v)|$. In this setting, vertices are considered to lie on a horizontal line and edges are drawn as semicircles above the line. There exist variants of MaxLA in which the arrangements are constrained. In the planar variant edge crossings are forbidden. In the projective variant for rooted trees arrangements are planar and the root cannot be covered by any edge. Here we present $O(n)$-time and $O(n)$-space algorithms that solve Planar and Projective MaxLA for trees. We also prove several properties of maximum projective and planar arrangements.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge