The optimality of syntactic dependency distances

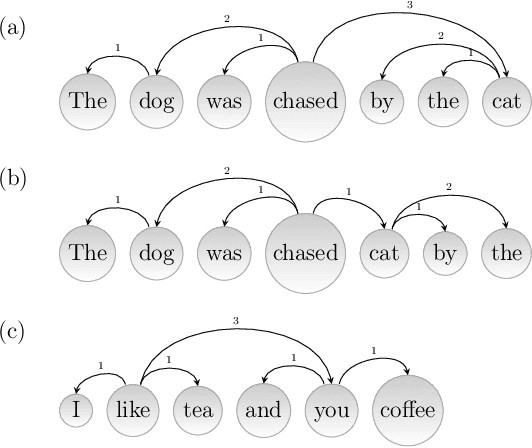
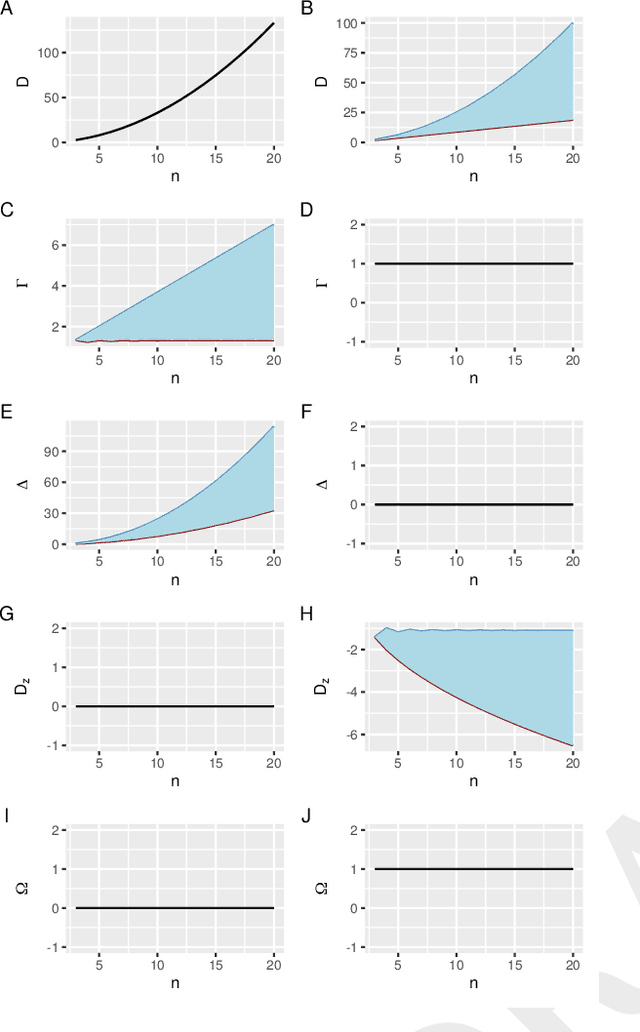
It is often stated that human languages, as other biological systems, are shaped by cost-cutting pressures but, to what extent? Attempts to quantify the degree of optimality of languages by means of an optimality score have been scarce and focused mostly on English. Here we recast the problem of the optimality of the word order of a sentence as an optimization problem on a spatial network where the vertices are words, arcs indicate syntactic dependencies and the space is defined by the linear order of the words in the sentence. We introduce a new score to quantify the cognitive pressure to reduce the distance between linked words in a sentence. The analysis of sentences from 93 languages representing 19 linguistic families reveals that half of languages are optimized to a 70% or more. The score indicates that distances are not significantly reduced in a few languages and confirms two theoretical predictions, i.e. that longer sentences are more optimized and that distances are more likely to be longer than expected by chance in short sentences. We present a new hierarchical ranking of languages by their degree of optimization. The statistical advantages of the new score call for a reevaluation of the evolution of dependency distance over time in languages as well as the relationship between dependency distance and linguistic competence. Finally, the principles behind the design of the score can be extended to develop more powerful normalizations of topological distances or physical distances in more dimensions.