Let the Quantum Creep In: Designing Quantum Neural Network Models by Gradually Swapping Out Classical Components

Artificial Intelligence (AI), with its multiplier effect and wide applications in multiple areas, could potentially be an important application of quantum computing. Since modern AI systems are often built on neural networks, the design of quantum neural networks becomes a key challenge in integrating quantum computing into AI. To provide a more fine-grained characterisation of the impact of quantum components on the performance of neural networks, we propose a framework where classical neural network layers are gradually replaced by quantum layers that have the same type of input and output while keeping the flow of information between layers unchanged, different from most current research in quantum neural network, which favours an end-to-end quantum model. We start with a simple three-layer classical neural network without any normalisation layers or activation functions, and gradually change the classical layers to the corresponding quantum versions. We conduct numerical experiments on image classification datasets such as the MNIST, FashionMNIST and CIFAR-10 datasets to demonstrate the change of performance brought by the systematic introduction of quantum components. Through this framework, our research sheds new light on the design of future quantum neural network models where it could be more favourable to search for methods and frameworks that harness the advantages from both the classical and quantum worlds.

Quantum Hamiltonian Embedding of Images for Data Reuploading Classifiers

When applying quantum computing to machine learning tasks, one of the first considerations is the design of the quantum machine learning model itself. Conventionally, the design of quantum machine learning algorithms relies on the ``quantisation" of classical learning algorithms, such as using quantum linear algebra to implement important subroutines of classical algorithms, if not the entire algorithm, seeking to achieve quantum advantage through possible run-time accelerations brought by quantum computing. However, recent research has started questioning whether quantum advantage via speedup is the right goal for quantum machine learning [1]. Research also has been undertaken to exploit properties that are unique to quantum systems, such as quantum contextuality, to better design quantum machine learning models [2]. In this paper, we take an alternative approach by incorporating the heuristics and empirical evidences from the design of classical deep learning algorithms to the design of quantum neural networks. We first construct a model based on the data reuploading circuit [3] with the quantum Hamiltonian data embedding unitary [4]. Through numerical experiments on images datasets, including the famous MNIST and FashionMNIST datasets, we demonstrate that our model outperforms the quantum convolutional neural network (QCNN)[5] by a large margin (up to over 40% on MNIST test set). Based on the model design process and numerical results, we then laid out six principles for designing quantum machine learning models, especially quantum neural networks.

Towards quantum enhanced adversarial robustness in machine learning

Machine learning algorithms are powerful tools for data driven tasks such as image classification and feature detection, however their vulnerability to adversarial examples - input samples manipulated to fool the algorithm - remains a serious challenge. The integration of machine learning with quantum computing has the potential to yield tools offering not only better accuracy and computational efficiency, but also superior robustness against adversarial attacks. Indeed, recent work has employed quantum mechanical phenomena to defend against adversarial attacks, spurring the rapid development of the field of quantum adversarial machine learning (QAML) and potentially yielding a new source of quantum advantage. Despite promising early results, there remain challenges towards building robust real-world QAML tools. In this review we discuss recent progress in QAML and identify key challenges. We also suggest future research directions which could determine the route to practicality for QAML approaches as quantum computing hardware scales up and noise levels are reduced.

GASP -- A Genetic Algorithm for State Preparation

The efficient preparation of quantum states is an important step in the execution of many quantum algorithms. In the noisy intermediate-scale quantum (NISQ) computing era, this is a significant challenge given quantum resources are scarce and typically only low-depth quantum circuits can be implemented on physical devices. We present a genetic algorithm for state preparation (GASP) which generates relatively low-depth quantum circuits for initialising a quantum computer in a specified quantum state. The method uses a basis set of R_x, R_y, R_z, and CNOT gates and a genetic algorithm to systematically generate circuits to synthesize the target state to the required fidelity. GASP can produce more efficient circuits of a given accuracy with lower depth and gate counts than other methods. This variability of the required accuracy facilitates overall higher accuracy on implementation, as error accumulation in high-depth circuits can be avoided. We directly compare the method to the state initialisation technique based on an exact synthesis technique by implemented in IBM Qiskit simulated with noise and implemented on physical IBM Quantum devices. Results achieved by GASP outperform Qiskit's exact general circuit synthesis method on a variety of states such as Gaussian states and W-states, and consistently show the method reduces the number of gates required for the quantum circuits to generate these quantum states to the required accuracy.

Benchmarking Adversarially Robust Quantum Machine Learning at Scale

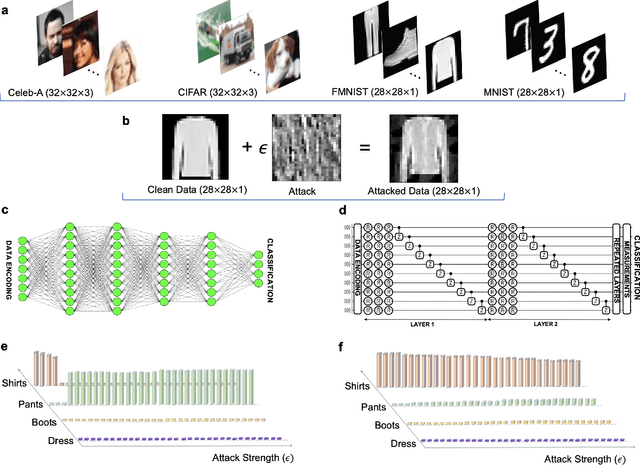
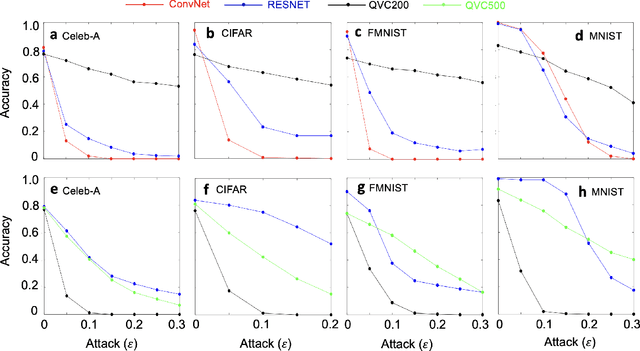
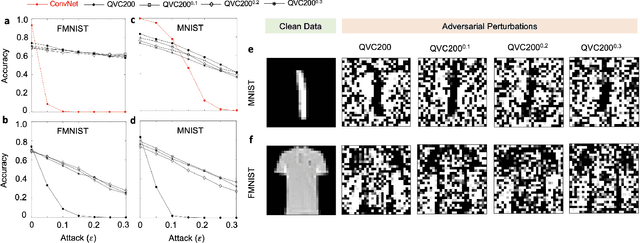
Machine learning (ML) methods such as artificial neural networks are rapidly becoming ubiquitous in modern science, technology and industry. Despite their accuracy and sophistication, neural networks can be easily fooled by carefully designed malicious inputs known as adversarial attacks. While such vulnerabilities remain a serious challenge for classical neural networks, the extent of their existence is not fully understood in the quantum ML setting. In this work, we benchmark the robustness of quantum ML networks, such as quantum variational classifiers (QVC), at scale by performing rigorous training for both simple and complex image datasets and through a variety of high-end adversarial attacks. Our results show that QVCs offer a notably enhanced robustness against classical adversarial attacks by learning features which are not detected by the classical neural networks, indicating a possible quantum advantage for ML tasks. Contrarily, and remarkably, the converse is not true, with attacks on quantum networks also capable of deceiving classical neural networks. By combining quantum and classical network outcomes, we propose a novel adversarial attack detection technology. Traditionally quantum advantage in ML systems has been sought through increased accuracy or algorithmic speed-up, but our work has revealed the potential for a new kind of quantum advantage through superior robustness of ML models, whose practical realisation will address serious security concerns and reliability issues of ML algorithms employed in a myriad of applications including autonomous vehicles, cybersecurity, and surveillance robotic systems.

A kernel-based quantum random forest for improved classification

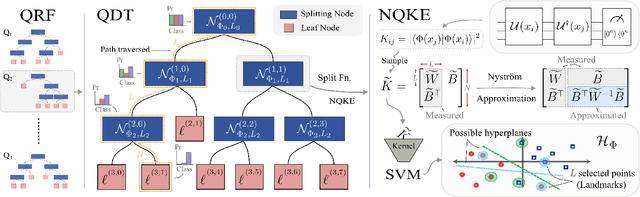
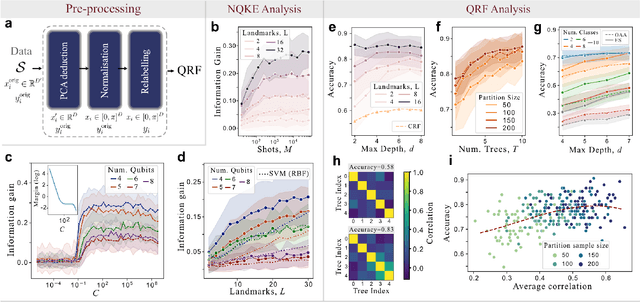
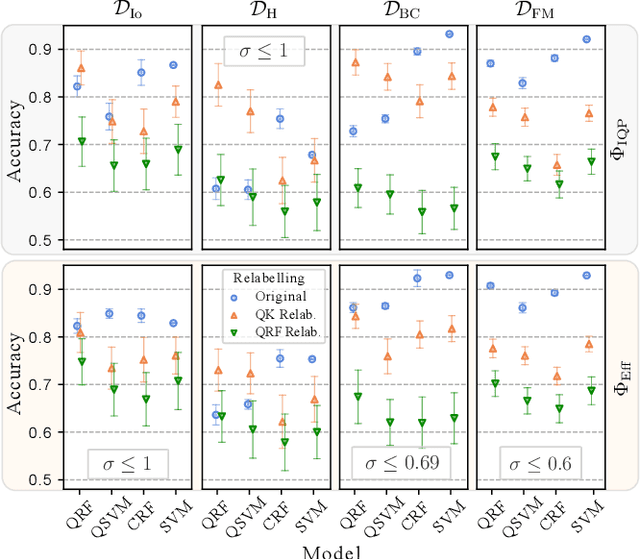
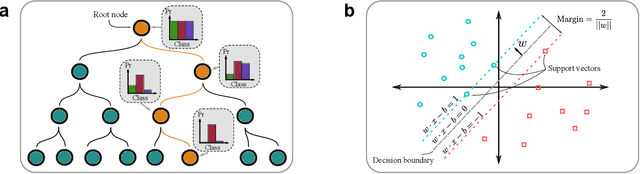
The emergence of Quantum Machine Learning (QML) to enhance traditional classical learning methods has seen various limitations to its realisation. There is therefore an imperative to develop quantum models with unique model hypotheses to attain expressional and computational advantage. In this work we extend the linear quantum support vector machine (QSVM) with kernel function computed through quantum kernel estimation (QKE), to form a decision tree classifier constructed from a decision directed acyclic graph of QSVM nodes - the ensemble of which we term the quantum random forest (QRF). To limit overfitting, we further extend the model to employ a low-rank Nystr\"{o}m approximation to the kernel matrix. We provide generalisation error bounds on the model and theoretical guarantees to limit errors due to finite sampling on the Nystr\"{o}m-QKE strategy. In doing so, we show that we can achieve lower sampling complexity when compared to QKE. We numerically illustrate the effect of varying model hyperparameters and finally demonstrate that the QRF is able obtain superior performance over QSVMs, while also requiring fewer kernel estimations.

Automated Quantum Circuit Design with Nested Monte Carlo Tree Search

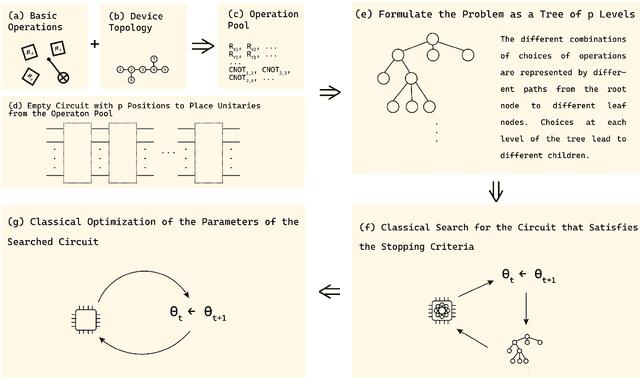
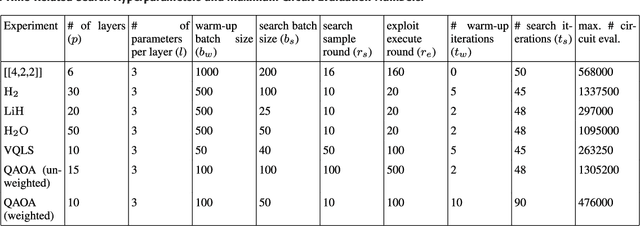
Quantum algorithms based on variational approaches are one of the most promising methods to construct quantum solutions and have found a myriad of applications in the last few years. Despite the adaptability and simplicity, their scalability and the selection of suitable ans\"atzs remain key challenges. In this work, we report an algorithmic framework based on nested Monte-Carlo Tree Search (MCTS) coupled with the combinatorial multi-armed bandit (CMAB) model for the automated design of quantum circuits. Through numerical experiments, we demonstrated our algorithm applied to various kinds of problems, including the ground energy problem in quantum chemistry, quantum optimisation on a graph, solving systems of linear equations, and finding encoding circuit for quantum error detection codes. Compared to the existing approaches, the results indicate that our circuit design algorithm can explore larger search spaces and optimise quantum circuits for larger systems, showing both versatility and scalability.

A scalable and fast artificial neural network syndrome decoder for surface codes

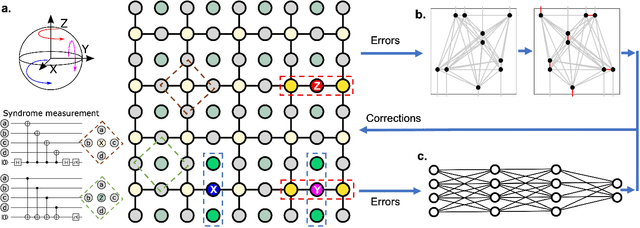
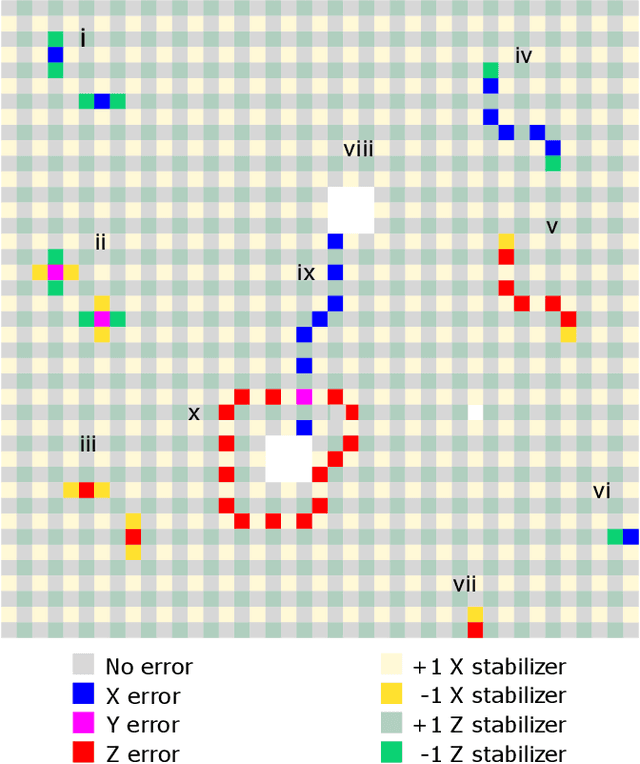
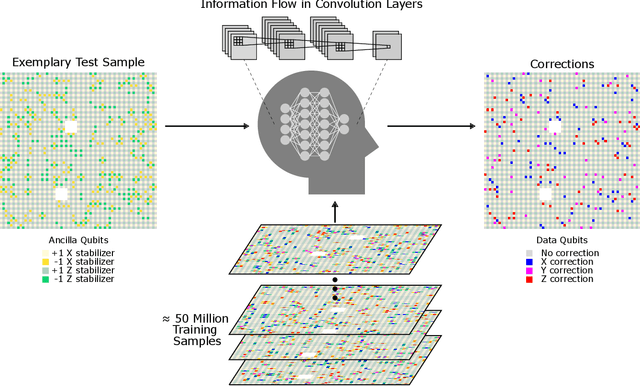
Surface code error correction offers a highly promising pathway to achieve scalable fault-tolerant quantum computing. When operated as stabilizer codes, surface code computations consist of a syndrome decoding step where measured stabilizer operators are used to determine appropriate corrections for errors in physical qubits. Decoding algorithms have undergone substantial development, with recent work incorporating machine learning (ML) techniques. Despite promising initial results, the ML-based syndrome decoders are still limited to small scale demonstrations with low latency and are incapable of handling surface codes with boundary conditions and various shapes needed for lattice surgery and braiding. Here, we report the development of an artificial neural network (ANN) based scalable and fast syndrome decoder capable of decoding surface codes of arbitrary shape and size with data qubits suffering from the depolarizing error model. Based on rigorous training over 50 million random quantum error instances, our ANN decoder is shown to work with code distances exceeding 1000 (more than 4 million physical qubits), which is the largest ML-based decoder demonstration to-date. The established ANN decoder demonstrates an execution time in principle independent of code distance, implying that its implementation on dedicated hardware could potentially offer surface code decoding times of O($\mu$sec), commensurate with the experimentally realisable qubit coherence times. With the anticipated scale-up of quantum processors within the next decade, their augmentation with a fast and scalable syndrome decoder such as developed in our work is expected to play a decisive role towards experimental implementation of fault-tolerant quantum information processing.