Quantum Spectral Model: Data Reuploading with Input-Conditioned Frequency Support

A central design principle in modern machine learning and artificial intelligence is to align a model's inductive bias with the structure of its input data. For matrix-valued inputs, relevant matrix-level relationships can be characterised through spectral values and spectral subspaces; however, common coordinate-wise rotation-gate data-encoding unitaries used in most quantum machine learning models do not explicitly construct such a matrix-level representation. We introduce Quantum Spectral Models (QSMs), in which we construct the generator of the data-encoding unitary directly from each input matrix. We study three QSM variants based on symmetric, global block, and non-overlapping patch-local block Hamiltonians. Their outputs admit truncated Fourier representations in which input-dependent spectral gaps supply candidate phase carriers, while spectral subspaces help determine their coefficients. We evaluate the QSMs and comparison quantum models on two matrix representations of Pendigits and two controlled synthetic tasks defined by spectral statistics. At the largest evaluated circuit depth, QSM variants lead the tested quantum models in mean test accuracy across all four benchmarks. The patch-local QSM leads on Pendigits, whereas the global block-Hamiltonian QSM leads on the controlled spectral tasks. Ablations show a task-dependent reversal: subspace-preserving controls perform better on Pendigits, whereas spectral-value-only controls lead among the tested ablations on the synthetic tasks. Together, these results shed new light on quantum machine-learning model design by showing how input-conditioned spectral representations can provide an analysable inductive bias, while offering a broader perspective on structure-aware model design in machine learning and artificial intelligence.

When cheap gradients fail: the measurement cost of attacking quantum classifiers

Adversarial perturbations threaten machine learning classifiers, including variational quantum classifiers. We show that finite quantum measurement statistics (shot noise) act as a built-in defense against gradient-based test-time attacks whose cost scales unfavorably for the attacker. Because every gradient component must be inferred from repeated circuit executions under any unbiased gradient-estimation rule, white-box extraction consumes a dimension-dependent measurement budget that measurement grouping cannot remove in expressive circuits. Under stated assumptions, single-step attacks need at least quadratically many shots in the input dimension $d$, growing as $d^{5/2}$ under norm-concentration scaling, with a sufficient-budget analysis for iterative attacks via stochastic gradient Langevin dynamics. Simulations up to 784 input dimensions validate the law: the realized total budget is the $d^{5/2}$ geometric floor for plateau-mitigated models and grows as $d^{3.00}$ for the tested deep circuits, whose gradient norms decay with dimension absent barren-plateau mitigation; folding the measured gradient norm back in recovers the parameter-free $d^{3/2}$ shot-noise geometry. Against a matched classical baseline whose attack overhead is dimension-independent (the cheap-gradient principle of automatic differentiation), the quantum gradient cost ratio grows empirically as $d^{3.00}$, so the attacker's relative cost diverges as the model scales. Experiments on a 156-qubit IBM processor (ibm_boston, 4-qubit circuits, $d=12$) reproduce the effect: at matched budgets the device attack tracks the ideal within a few percent, with the high-shot gradient faithful to the exact one. The defense operates precisely when the forward map is classically hard to simulate: only then is a white-box attacker denied the simulate-and-backpropagate shortcut and must pay the measurement cost we quantify.

Fine-Tuning Large Language Models for Quantum Reasoning

Large language models (LLMs) exhibit abilities beyond natural language modelling and text generation. Recent advances in their reasoning capabilities have spurred interest in applying LLMs to complex scientific tasks requiring deep domain expertise and sophisticated reasoning. Quantum computing, as a highly specialised field with significant knowledge barriers and hardware constraints, could greatly benefit from such advancements. However, a key open question that first must be answered is: How can we develop fine-tuning pipelines that instil genuine quantum reasoning in LLMs, rather than task-specific pattern matching? We study this question through quantum circuit simulation as a training objective, where the model must predict the measurement probability distribution resulting from a sequence of quantum gate operations. We propose and compare two fine-tuning pipelines: (1) Supervised Fine-Tuning (SFT) on explicit gate-by-gate state-vector simulation traces, and (2) a two-stage SFT+Group Relative Policy Optimisation (GRPO) approach that sequentially applies SFT followed by GRPO with verifiable rewards. Our findings show that SFT achieves near-perfect in-distribution and gate-count extrapolation accuracy, significantly outperforming both the base model and the GPT-OSS-120B baseline. SFT+GRPO trades some in-distribution precision for better generalisation to larger qubit systems that SFT alone cannot handle. Both pipelines significantly outperform the baselines, demonstrating that targeted fine-tuning on explicit reasoning traces is an effective strategy for advancing quantum reasoning in LLMs.

MADQRL: Distributed Quantum Reinforcement Learning Framework for Multi-Agent Environments

Reinforcement learning (RL) is one of the most practical ways to learn from real-life use-cases. Motivated from the cognitive methods used by humans makes it a widely acceptable strategy in the field of artificial intelligence. Most of the environments used for RL are often high-dimensional, and traditional RL algorithms becomes computationally expensive and challenging to effectively learn from such systems. Recent advancements in practical demonstration of quantum computing (QC) theories, such as compact encoding, enhanced representation and learning algorithms, random sampling, or the inherent stochastic nature of quantum systems, have opened up new directions to tackle these challenges. Quantum reinforcement learning (QRL) is seeking significant traction over the past few years. However, the current state of quantum hardware is not enough to cater for such high-dimensional environments with complex multi-agent setup. To tackle this issue, we propose a distributed framework for QRL where multiple agents learn independently, distributing the load of joint training from individual machines. Our method works well for environments with disjoint sets of action and observation spaces, but can also be extended to other systems with reasonable approximations. We analyze the proposed method on cooperative-pong environment and our results indicate ~10% improvement from other distribution strategies, and ~5% improvement from classical models of policy representation.

Adam assisted Fully informed Particle Swarm Optimzation ( Adam-FIPSO ) based Parameter Prediction for the Quantum Approximate Optimization Algorithm (QAOA)

The Quantum Approximate Optimization Algorithm (QAOA) is a prominent variational algorithm used for solving combinatorial optimization problems such as the Max-Cut problem. A key challenge in QAOA lies in efficiently identifying suitable parameters (gamma, beta) that lead to high-quality solutions. In this paper, we propose a framework that combines Fully Informed Particle Swarm Optimization (FIPSO) with adaptive gradient correction using the Adam Optimizer to navigate the QAOA parameter space. This approach aims to avoid issues such as barren plateaus and convergence to local minima. The proposed algorithm is evaluated against two classes of graph instances, Erdos Renyi and Watts-Strogatz. Experimental results across multiple QAOA depths consistently demonstrate superior performance compared to random initialization, underscoring the effectiveness and robustness of the proposed optimization framework.

Computable Model-Independent Bounds for Adversarial Quantum Machine Learning

By leveraging the principles of quantum mechanics, QML opens doors to novel approaches in machine learning and offers potential speedup. However, machine learning models are well-documented to be vulnerable to malicious manipulations, and this susceptibility extends to the models of QML. This situation necessitates a thorough understanding of QML's resilience against adversarial attacks, particularly in an era where quantum computing capabilities are expanding. In this regard, this paper examines model-independent bounds on adversarial performance for QML. To the best of our knowledge, we introduce the first computation of an approximate lower bound for adversarial error when evaluating model resilience against sophisticated quantum-based adversarial attacks. Experimental results are compared to the computed bound, demonstrating the potential of QML models to achieve high robustness. In the best case, the experimental error is only 10% above the estimated bound, offering evidence of the inherent robustness of quantum models. This work not only advances our theoretical understanding of quantum model resilience but also provides a precise reference bound for the future development of robust QML algorithms.

Let the Quantum Creep In: Designing Quantum Neural Network Models by Gradually Swapping Out Classical Components

Artificial Intelligence (AI), with its multiplier effect and wide applications in multiple areas, could potentially be an important application of quantum computing. Since modern AI systems are often built on neural networks, the design of quantum neural networks becomes a key challenge in integrating quantum computing into AI. To provide a more fine-grained characterisation of the impact of quantum components on the performance of neural networks, we propose a framework where classical neural network layers are gradually replaced by quantum layers that have the same type of input and output while keeping the flow of information between layers unchanged, different from most current research in quantum neural network, which favours an end-to-end quantum model. We start with a simple three-layer classical neural network without any normalisation layers or activation functions, and gradually change the classical layers to the corresponding quantum versions. We conduct numerical experiments on image classification datasets such as the MNIST, FashionMNIST and CIFAR-10 datasets to demonstrate the change of performance brought by the systematic introduction of quantum components. Through this framework, our research sheds new light on the design of future quantum neural network models where it could be more favourable to search for methods and frameworks that harness the advantages from both the classical and quantum worlds.

Quantum Hamiltonian Embedding of Images for Data Reuploading Classifiers

When applying quantum computing to machine learning tasks, one of the first considerations is the design of the quantum machine learning model itself. Conventionally, the design of quantum machine learning algorithms relies on the ``quantisation" of classical learning algorithms, such as using quantum linear algebra to implement important subroutines of classical algorithms, if not the entire algorithm, seeking to achieve quantum advantage through possible run-time accelerations brought by quantum computing. However, recent research has started questioning whether quantum advantage via speedup is the right goal for quantum machine learning [1]. Research also has been undertaken to exploit properties that are unique to quantum systems, such as quantum contextuality, to better design quantum machine learning models [2]. In this paper, we take an alternative approach by incorporating the heuristics and empirical evidences from the design of classical deep learning algorithms to the design of quantum neural networks. We first construct a model based on the data reuploading circuit [3] with the quantum Hamiltonian data embedding unitary [4]. Through numerical experiments on images datasets, including the famous MNIST and FashionMNIST datasets, we demonstrate that our model outperforms the quantum convolutional neural network (QCNN)[5] by a large margin (up to over 40% on MNIST test set). Based on the model design process and numerical results, we then laid out six principles for designing quantum machine learning models, especially quantum neural networks.

Impact of Data Augmentation on QCNNs

In recent years, Classical Convolutional Neural Networks (CNNs) have been applied for image recognition successfully. Quantum Convolutional Neural Networks (QCNNs) are proposed as a novel generalization to CNNs by using quantum mechanisms. The quantum mechanisms lead to an efficient training process in QCNNs by reducing the size of input from $N$ to $log_2N$. This paper implements and compares both CNNs and QCNNs by testing losses and prediction accuracy on three commonly used datasets. The datasets include the MNIST hand-written digits, Fashion MNIST and cat/dog face images. Additionally, data augmentation (DA), a technique commonly used in CNNs to improve the performance of classification by generating similar images based on original inputs, is also implemented in QCNNs. Surprisingly, the results showed that data augmentation didn't improve QCNNs performance. The reasons and logic behind this result are discussed, hoping to expand our understanding of Quantum machine learning theory.

Automated Quantum Circuit Design with Nested Monte Carlo Tree Search

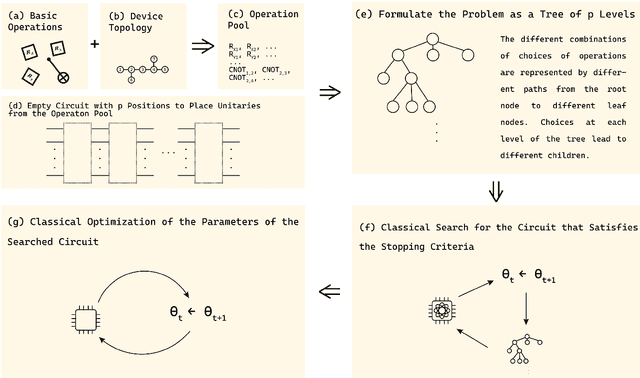
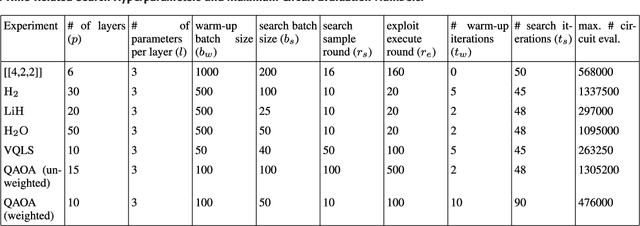
Quantum algorithms based on variational approaches are one of the most promising methods to construct quantum solutions and have found a myriad of applications in the last few years. Despite the adaptability and simplicity, their scalability and the selection of suitable ans\"atzs remain key challenges. In this work, we report an algorithmic framework based on nested Monte-Carlo Tree Search (MCTS) coupled with the combinatorial multi-armed bandit (CMAB) model for the automated design of quantum circuits. Through numerical experiments, we demonstrated our algorithm applied to various kinds of problems, including the ground energy problem in quantum chemistry, quantum optimisation on a graph, solving systems of linear equations, and finding encoding circuit for quantum error detection codes. Compared to the existing approaches, the results indicate that our circuit design algorithm can explore larger search spaces and optimise quantum circuits for larger systems, showing both versatility and scalability.