Towards quantum enhanced adversarial robustness in machine learning

Machine learning algorithms are powerful tools for data driven tasks such as image classification and feature detection, however their vulnerability to adversarial examples - input samples manipulated to fool the algorithm - remains a serious challenge. The integration of machine learning with quantum computing has the potential to yield tools offering not only better accuracy and computational efficiency, but also superior robustness against adversarial attacks. Indeed, recent work has employed quantum mechanical phenomena to defend against adversarial attacks, spurring the rapid development of the field of quantum adversarial machine learning (QAML) and potentially yielding a new source of quantum advantage. Despite promising early results, there remain challenges towards building robust real-world QAML tools. In this review we discuss recent progress in QAML and identify key challenges. We also suggest future research directions which could determine the route to practicality for QAML approaches as quantum computing hardware scales up and noise levels are reduced.

GASP -- A Genetic Algorithm for State Preparation

The efficient preparation of quantum states is an important step in the execution of many quantum algorithms. In the noisy intermediate-scale quantum (NISQ) computing era, this is a significant challenge given quantum resources are scarce and typically only low-depth quantum circuits can be implemented on physical devices. We present a genetic algorithm for state preparation (GASP) which generates relatively low-depth quantum circuits for initialising a quantum computer in a specified quantum state. The method uses a basis set of R_x, R_y, R_z, and CNOT gates and a genetic algorithm to systematically generate circuits to synthesize the target state to the required fidelity. GASP can produce more efficient circuits of a given accuracy with lower depth and gate counts than other methods. This variability of the required accuracy facilitates overall higher accuracy on implementation, as error accumulation in high-depth circuits can be avoided. We directly compare the method to the state initialisation technique based on an exact synthesis technique by implemented in IBM Qiskit simulated with noise and implemented on physical IBM Quantum devices. Results achieved by GASP outperform Qiskit's exact general circuit synthesis method on a variety of states such as Gaussian states and W-states, and consistently show the method reduces the number of gates required for the quantum circuits to generate these quantum states to the required accuracy.

A kernel-based quantum random forest for improved classification

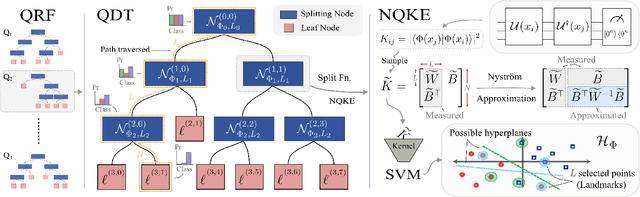
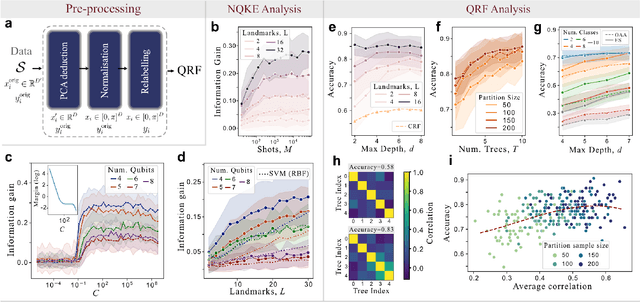
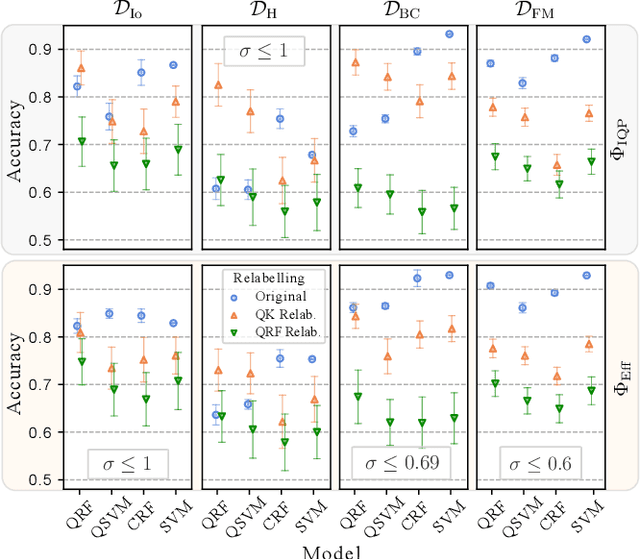
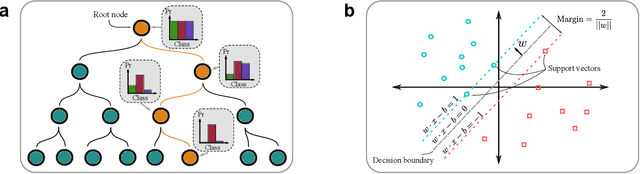
The emergence of Quantum Machine Learning (QML) to enhance traditional classical learning methods has seen various limitations to its realisation. There is therefore an imperative to develop quantum models with unique model hypotheses to attain expressional and computational advantage. In this work we extend the linear quantum support vector machine (QSVM) with kernel function computed through quantum kernel estimation (QKE), to form a decision tree classifier constructed from a decision directed acyclic graph of QSVM nodes - the ensemble of which we term the quantum random forest (QRF). To limit overfitting, we further extend the model to employ a low-rank Nystr\"{o}m approximation to the kernel matrix. We provide generalisation error bounds on the model and theoretical guarantees to limit errors due to finite sampling on the Nystr\"{o}m-QKE strategy. In doing so, we show that we can achieve lower sampling complexity when compared to QKE. We numerically illustrate the effect of varying model hyperparameters and finally demonstrate that the QRF is able obtain superior performance over QSVMs, while also requiring fewer kernel estimations.