Stability and Convergence of Stochastic Particle Flow Filters

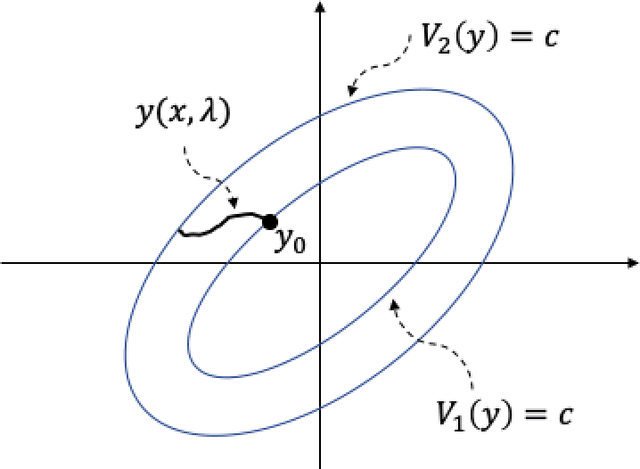
In this paper, we examine dynamic properties of particle flows for a recently derived parameterized family of stochastic particle flow filters for nonlinear filtering and Bayesian inference. In particular, we establish that particles maintain desired posterior distribution without the Gaussian assumption on measurement likelihood. Adopting the concept of Lyapunov stability, we further show that particles stay close but do not converge to the maximum likelihood estimate of the posterior distribution. The results demonstrate that stability of particle flows is maintained for this family of stochastic particle flow filters.

Stiffness Mitigation in Stochastic Particle Flow Filters

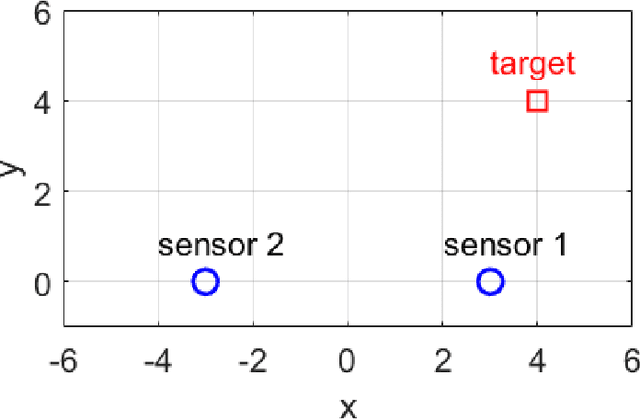
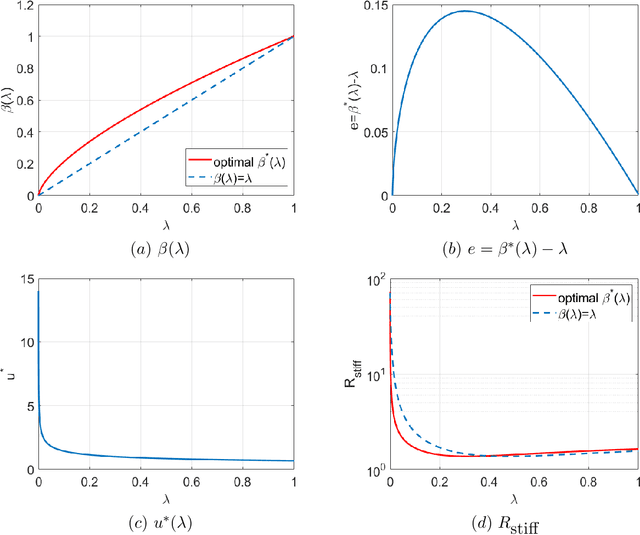
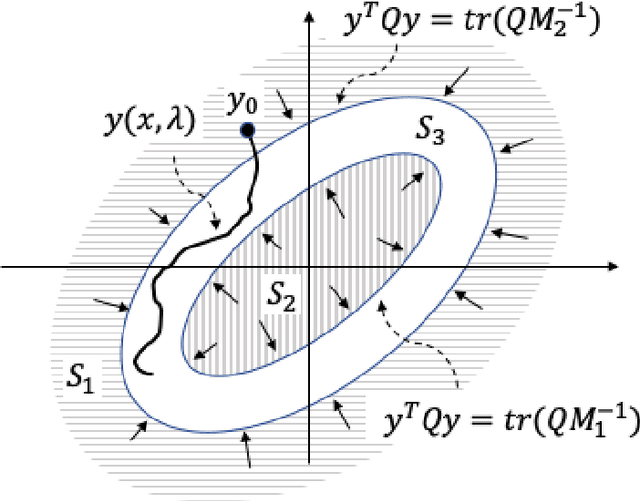
The linear convex log-homotopy has been used in the derivation of particle flow filters. One natural question is whether it is beneficial to consider other forms of homotopy. We revisit this question by considering a general linear form of log-homotopy for which we derive particle flow filters, validate the distribution of flows, and obtain conditions for the stability of particle flows. We then formulate the problem of stiffness mitigation as an optimal control problem by minimizing the condition number of the Hessian matrix of the posterior density function. The optimal homotopy can be efficiently obtained by solving a one-dimensional second order two-point boundary value problem. Compared with traditional matrix analysis based approaches to condition number improvements such as scaling, this novel approach explicitly exploits the special structure of the stochastic differential equations in particle flow filters. The effectiveness of the proposed approach is demonstrated by a numerical example.

A New Parameterized Family of Stochastic Particle Flow Filters

We derive a parameterized family of stochastic particle flows driven by a nonzero diffusion process for nonlinear filtering, Bayesian inference, or target tracking. This new family of stochastic flows takes the form of a linear combination of prior knowledge and measurement likelihood information. It is shown that several particle flows existing in the literature are special cases of this family. We prove that the particle flows are unbiased under the assumption of linear measurement and Gaussian distributions, and examine the consistency of estimates constructed from the stochastic flows. We further establish several finite time stability concepts for this new family of stochastic particle flows.

Community Detection and Improved Detectability in Multiplex Networks

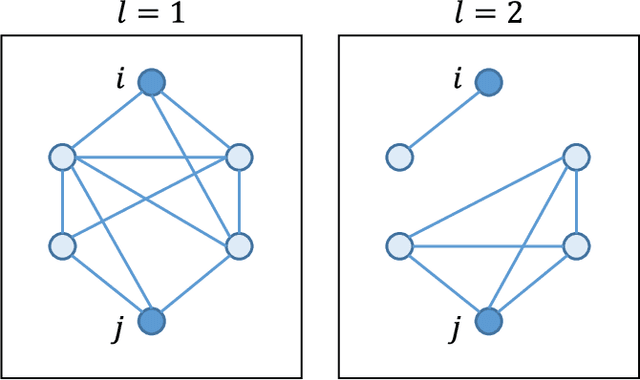
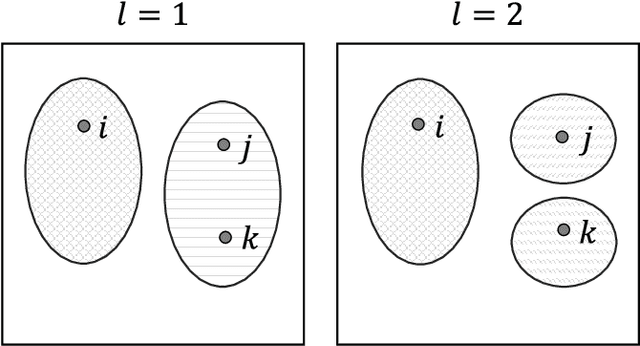
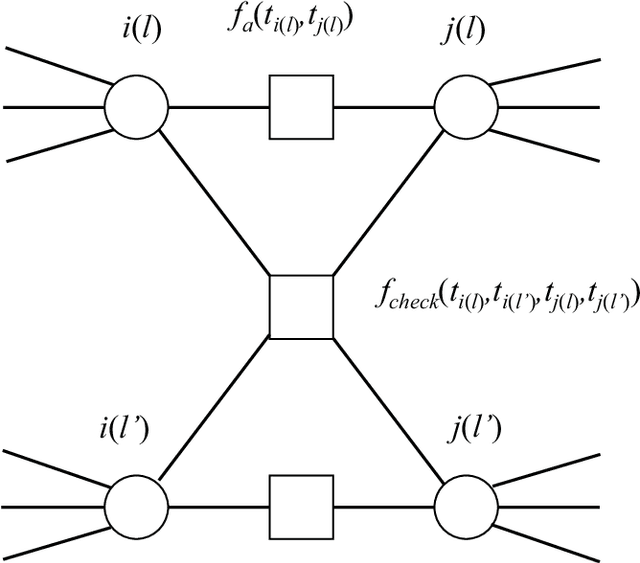
We investigate the widely encountered problem of detecting communities in multiplex networks, such as social networks, with an unknown arbitrary heterogeneous structure. To improve detectability, we propose a generative model that leverages the multiplicity of a single community in multiple layers, with no prior assumption on the relation of communities among different layers. Our model relies on a novel idea of incorporating a large set of generic localized community label constraints across the layers, in conjunction with the celebrated Stochastic Block Model (SBM) in each layer. Accordingly, we build a probabilistic graphical model over the entire multiplex network by treating the constraints as Bayesian priors. We mathematically prove that these constraints/priors promote existence of identical communities across layers without introducing further correlation between individual communities. The constraints are further tailored to render a sparse graphical model and the numerically efficient Belief Propagation algorithm is subsequently employed. We further demonstrate by numerical experiments that in the presence of consistent communities between different layers, consistent communities are matched, and the detectability is improved over a single layer. We compare our model with a "correlated model" which exploits the prior knowledge of community correlation between layers. Similar detectability improvement is obtained under such a correlation, even though our model relies on much milder assumptions than the correlated model. Our model even shows a better detection performance over a certain correlation and signal to noise ratio (SNR) range. In the absence of community correlation, the correlation model naturally fails, while ours maintains its performance.

Analysis Dictionary Learning: An Efficient and Discriminative Solution

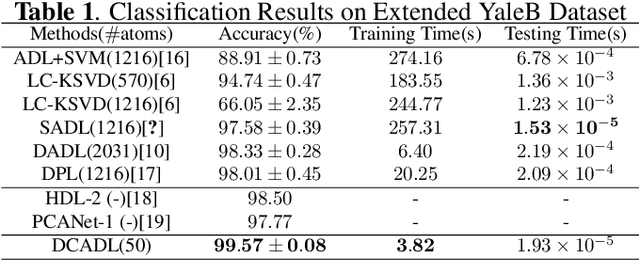
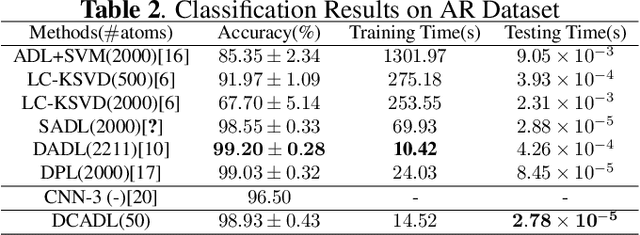
Discriminative Dictionary Learning (DL) methods have been widely advocated for image classification problems. To further sharpen their discriminative capabilities, most state-of-the-art DL methods have additional constraints included in the learning stages. These various constraints, however, lead to additional computational complexity. We hence propose an efficient Discriminative Convolutional Analysis Dictionary Learning (DCADL) method, as a lower cost Discriminative DL framework, to both characterize the image structures and refine the interclass structure representations. The proposed DCADL jointly learns a convolutional analysis dictionary and a universal classifier, while greatly reducing the time complexity in both training and testing phases, and achieving a competitive accuracy, thus demonstrating great performance in many experiments with standard databases.

Analysis Dictionary Learning based Classification: Structure for Robustness

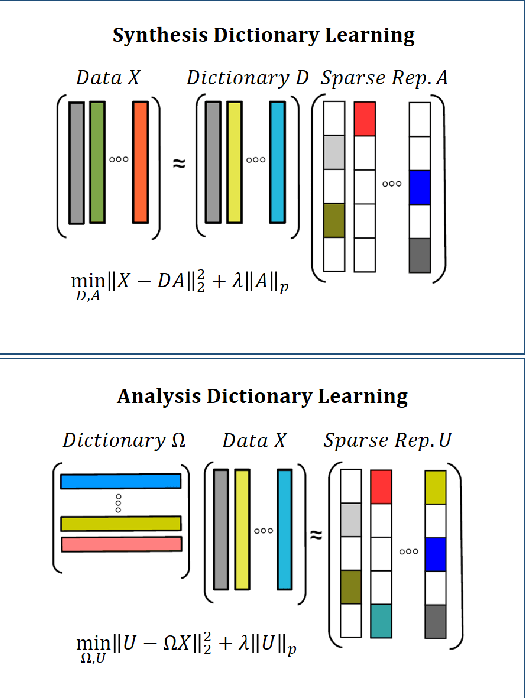
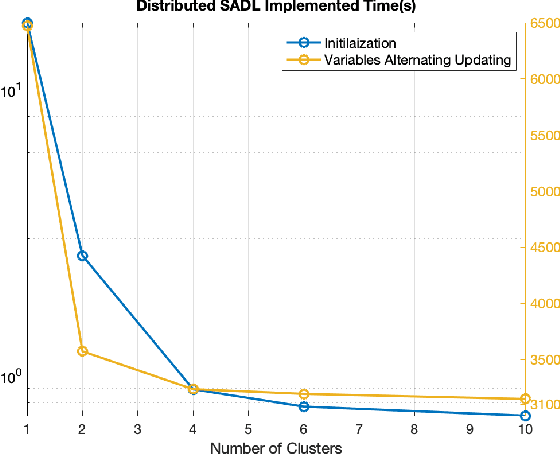
A discriminative structured analysis dictionary is proposed for the classification task. A structure of the union of subspaces (UoS) is integrated into the conventional analysis dictionary learning to enhance the capability of discrimination. A simple classifier is also simultaneously included into the formulated functional to ensure a more complete consistent classification. The solution of the algorithm is efficiently obtained by the linearized alternating direction method of multipliers. Moreover, a distributed structured analysis dictionary learning is also presented to address large scale datasets. It can group-(class-) independently train the structured analysis dictionaries by different machines/cores/threads, and therefore avoid a high computational cost. A consensus structured analysis dictionary and a global classifier are jointly learned in the distributed approach to safeguard the discriminative power and the efficiency of classification. Experiments demonstrate that our method achieves a comparable or better performance than the state-of-the-art algorithms in a variety of visual classification tasks. In addition, the training and testing computational complexity are also greatly reduced.

Structured Analysis Dictionary Learning for Image Classification

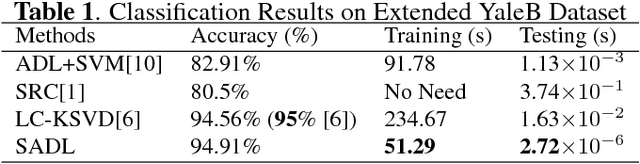
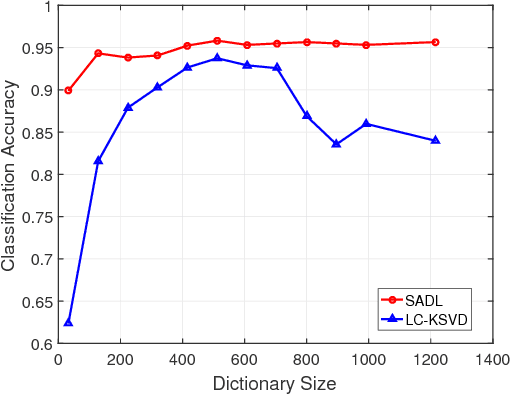
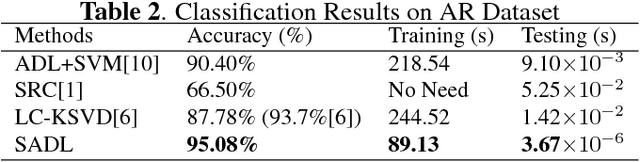
We propose a computationally efficient and high-performance classification algorithm by incorporating class structural information in analysis dictionary learning. To achieve more consistent classification, we associate a class characteristic structure of independent subspaces and impose it on the classification error constrained analysis dictionary learning. Experiments demonstrate that our method achieves a comparable or better performance than the state-of-the-art algorithms in a variety of visual classification tasks. In addition, our method greatly reduces the training and testing computational complexity.

Demystifying Deep Learning: A Geometric Approach to Iterative Projections

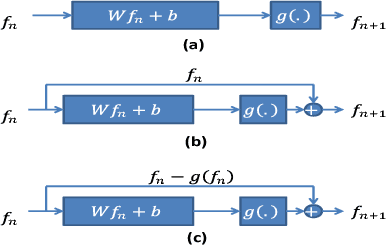
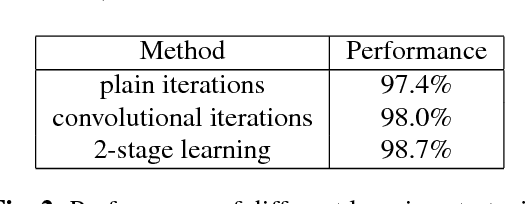
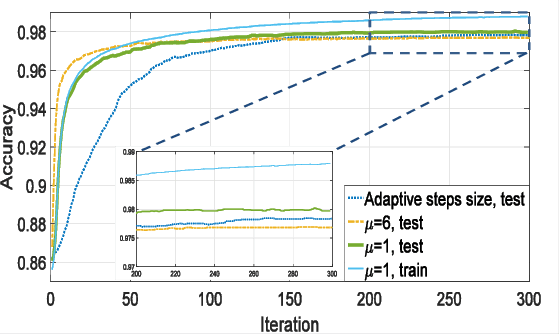
Parametric approaches to Learning, such as deep learning (DL), are highly popular in nonlinear regression, in spite of their extremely difficult training with their increasing complexity (e.g. number of layers in DL). In this paper, we present an alternative semi-parametric framework which foregoes the ordinarily required feedback, by introducing the novel idea of geometric regularization. We show that certain deep learning techniques such as residual network (ResNet) architecture are closely related to our approach. Hence, our technique can be used to analyze these types of deep learning. Moreover, we present preliminary results which confirm that our approach can be easily trained to obtain complex structures.

Deep Dictionary Learning: A PARametric NETwork Approach

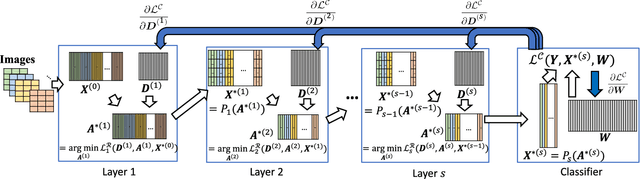
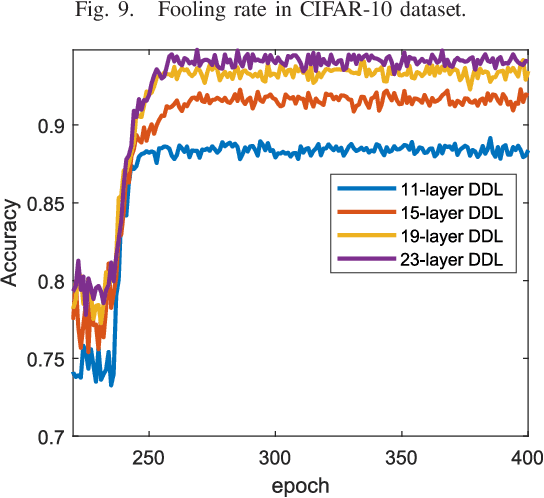
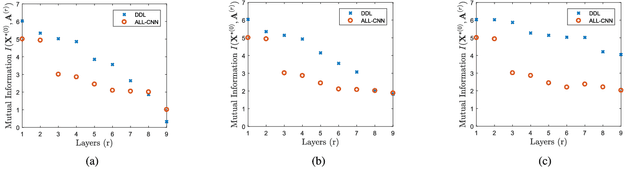
Deep dictionary learning seeks multiple dictionaries at different image scales to capture complementary coherent characteristics. We propose a method for learning a hierarchy of synthesis dictionaries with an image classification goal. The dictionaries and classification parameters are trained by a classification objective, and the sparse features are extracted by reducing a reconstruction loss in each layer. The reconstruction objectives in some sense regularize the classification problem and inject source signal information in the extracted features. The performance of the proposed hierarchical method increases by adding more layers, which consequently makes this model easier to tune and adapt. The proposed algorithm furthermore, shows remarkably lower fooling rate in presence of adversarial perturbation. The validation of the proposed approach is based on its classification performance using four benchmark datasets and is compared to a CNN of similar size.