Stiffness Mitigation in Stochastic Particle Flow Filters

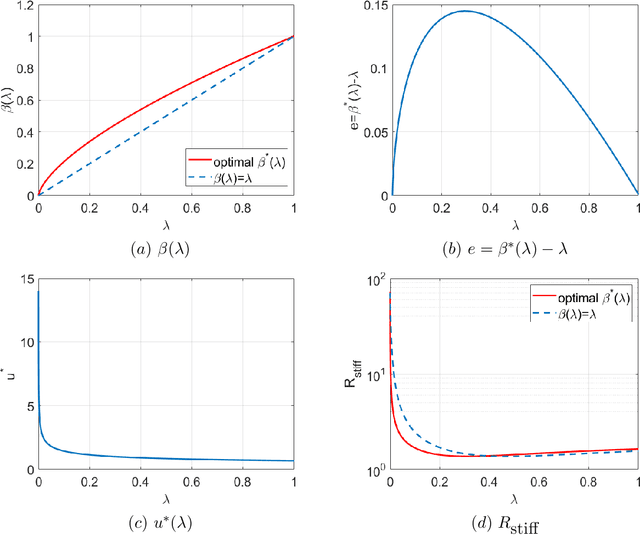
The linear convex log-homotopy has been used in the derivation of particle flow filters. One natural question is whether it is beneficial to consider other forms of homotopy. We revisit this question by considering a general linear form of log-homotopy for which we derive particle flow filters, validate the distribution of flows, and obtain conditions for the stability of particle flows. We then formulate the problem of stiffness mitigation as an optimal control problem by minimizing the condition number of the Hessian matrix of the posterior density function. The optimal homotopy can be efficiently obtained by solving a one-dimensional second order two-point boundary value problem. Compared with traditional matrix analysis based approaches to condition number improvements such as scaling, this novel approach explicitly exploits the special structure of the stochastic differential equations in particle flow filters. The effectiveness of the proposed approach is demonstrated by a numerical example.

A New Parameterized Family of Stochastic Particle Flow Filters

We derive a parameterized family of stochastic particle flows driven by a nonzero diffusion process for nonlinear filtering, Bayesian inference, or target tracking. This new family of stochastic flows takes the form of a linear combination of prior knowledge and measurement likelihood information. It is shown that several particle flows existing in the literature are special cases of this family. We prove that the particle flows are unbiased under the assumption of linear measurement and Gaussian distributions, and examine the consistency of estimates constructed from the stochastic flows. We further establish several finite time stability concepts for this new family of stochastic particle flows.