Get our free extension to see links to code for papers anywhere online!Free add-on: code for papers everywhere!Free add-on: See code for papers anywhere!
Fred Daum
Stability and Convergence of Stochastic Particle Flow Filters
Aug 11, 2021Figures and Tables: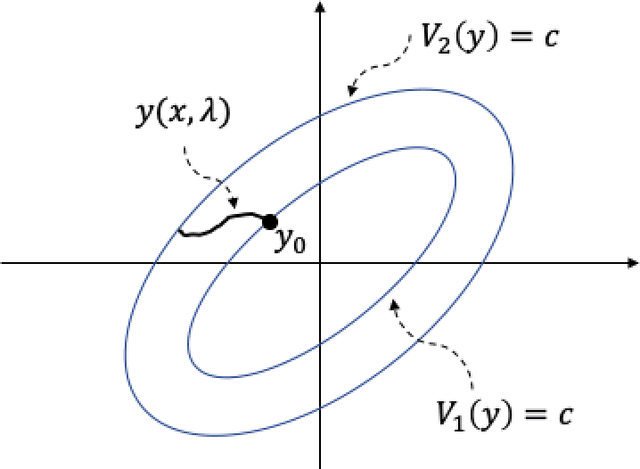
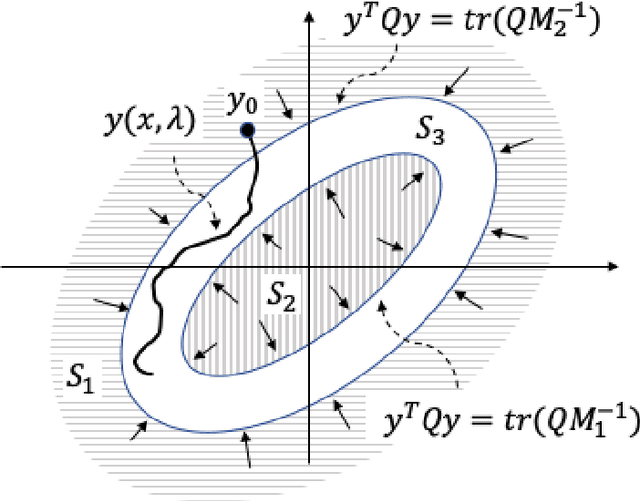


Abstract:In this paper, we examine dynamic properties of particle flows for a recently derived parameterized family of stochastic particle flow filters for nonlinear filtering and Bayesian inference. In particular, we establish that particles maintain desired posterior distribution without the Gaussian assumption on measurement likelihood. Adopting the concept of Lyapunov stability, we further show that particles stay close but do not converge to the maximum likelihood estimate of the posterior distribution. The results demonstrate that stability of particle flows is maintained for this family of stochastic particle flow filters.
Via
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge