Community Detection and Improved Detectability in Multiplex Networks
Paper and Code
Sep 23, 2019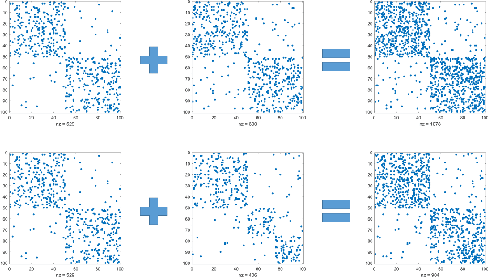
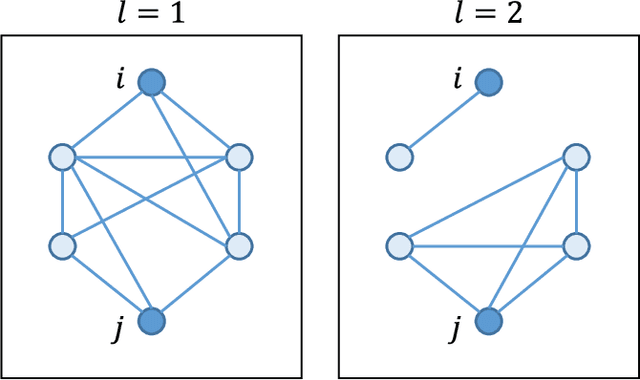
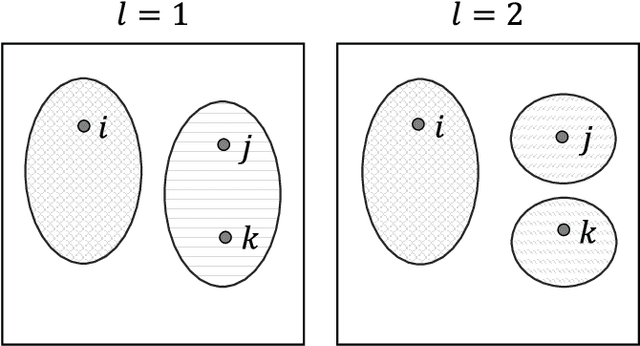
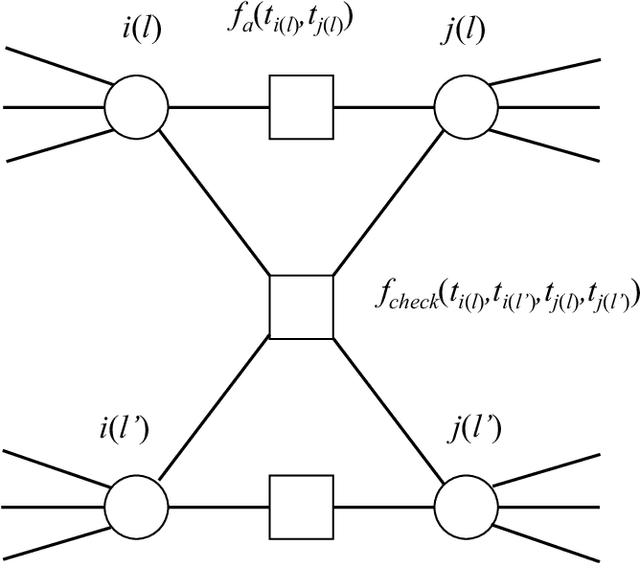
We investigate the widely encountered problem of detecting communities in multiplex networks, such as social networks, with an unknown arbitrary heterogeneous structure. To improve detectability, we propose a generative model that leverages the multiplicity of a single community in multiple layers, with no prior assumption on the relation of communities among different layers. Our model relies on a novel idea of incorporating a large set of generic localized community label constraints across the layers, in conjunction with the celebrated Stochastic Block Model (SBM) in each layer. Accordingly, we build a probabilistic graphical model over the entire multiplex network by treating the constraints as Bayesian priors. We mathematically prove that these constraints/priors promote existence of identical communities across layers without introducing further correlation between individual communities. The constraints are further tailored to render a sparse graphical model and the numerically efficient Belief Propagation algorithm is subsequently employed. We further demonstrate by numerical experiments that in the presence of consistent communities between different layers, consistent communities are matched, and the detectability is improved over a single layer. We compare our model with a "correlated model" which exploits the prior knowledge of community correlation between layers. Similar detectability improvement is obtained under such a correlation, even though our model relies on much milder assumptions than the correlated model. Our model even shows a better detection performance over a certain correlation and signal to noise ratio (SNR) range. In the absence of community correlation, the correlation model naturally fails, while ours maintains its performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge