Compatibility of Fairness Metrics with EU Non-Discrimination Laws: Demographic Parity & Conditional Demographic Disparity

Empirical evidence suggests that algorithmic decisions driven by Machine Learning (ML) techniques threaten to discriminate against legally protected groups or create new sources of unfairness. This work supports the contextual approach to fairness in EU non-discrimination legal framework and aims at assessing up to what point we can assure legal fairness through fairness metrics and under fairness constraints. For that, we analyze the legal notion of non-discrimination and differential treatment with the fairness definition Demographic Parity (DP) through Conditional Demographic Disparity (CDD). We train and compare different classifiers with fairness constraints to assess whether it is possible to reduce bias in the prediction while enabling the contextual approach to judicial interpretation practiced under EU non-discrimination laws. Our experimental results on three scenarios show that the in-processing bias mitigation algorithm leads to different performances in each of them. Our experiments and analysis suggest that AI-assisted decision-making can be fair from a legal perspective depending on the case at hand and the legal justification. These preliminary results encourage future work which will involve further case studies, metrics, and fairness notions.

Measuring Implicit Bias Using SHAP Feature Importance and Fuzzy Cognitive Maps

In this paper, we integrate the concepts of feature importance with implicit bias in the context of pattern classification. This is done by means of a three-step methodology that involves (i) building a classifier and tuning its hyperparameters, (ii) building a Fuzzy Cognitive Map model able to quantify implicit bias, and (iii) using the SHAP feature importance to active the neural concepts when performing simulations. The results using a real case study concerning fairness research support our two-fold hypothesis. On the one hand, it is illustrated the risks of using a feature importance method as an absolute tool to measure implicit bias. On the other hand, it is concluded that the amount of bias towards protected features might differ depending on whether the features are numerically or categorically encoded.

Modeling Implicit Bias with Fuzzy Cognitive Maps

This paper presents a Fuzzy Cognitive Map model to quantify implicit bias in structured datasets where features can be numeric or discrete. In our proposal, problem features are mapped to neural concepts that are initially activated by experts when running what-if simulations, whereas weights connecting the neural concepts represent absolute correlation/association patterns between features. In addition, we introduce a new reasoning mechanism equipped with a normalization-like transfer function that prevents neurons from saturating. Another advantage of this new reasoning mechanism is that it can easily be controlled by regulating nonlinearity when updating neurons' activation values in each iteration. Finally, we study the convergence of our model and derive analytical conditions concerning the existence and unicity of fixed-point attractors.

A fuzzy-rough uncertainty measure to discover bias encoded explicitly or implicitly in features of structured pattern classification datasets

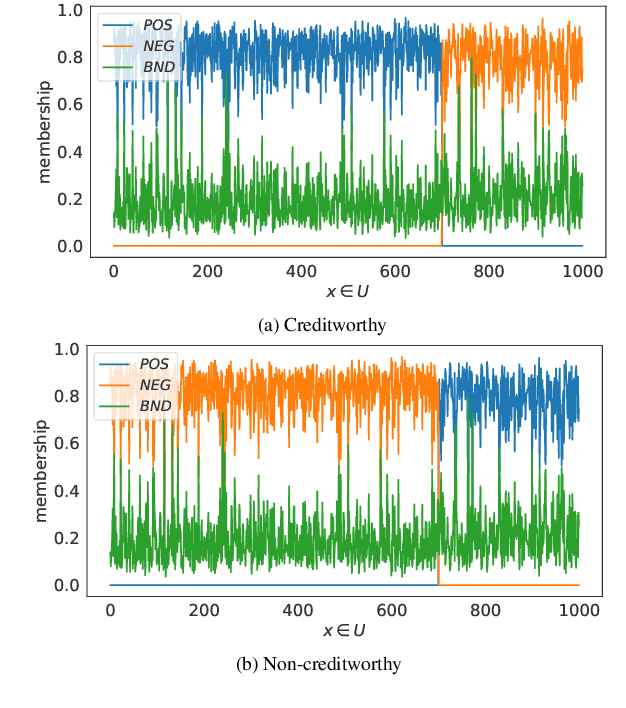
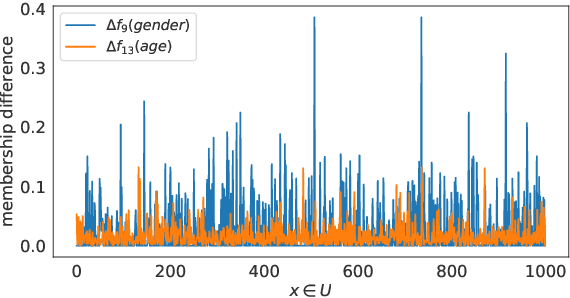
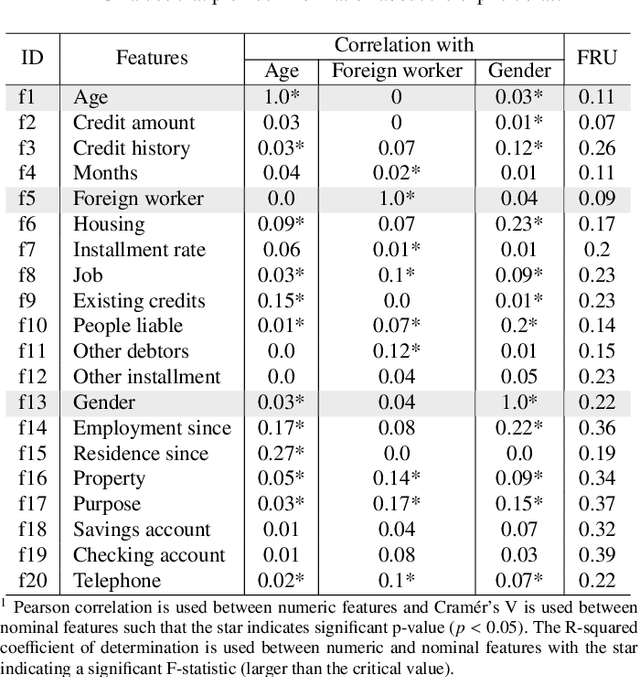
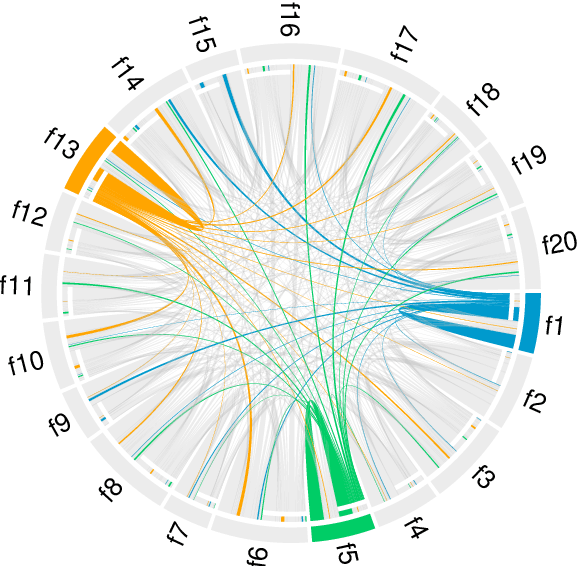
The need to measure bias encoded in tabular data that are used to solve pattern recognition problems is widely recognized by academia, legislators and enterprises alike. In previous work, we proposed a bias quantification measure, called fuzzy-rough uncer-tainty, which relies on the fuzzy-rough set theory. The intuition dictates that protected features should not change the fuzzy-rough boundary regions of a decision class significantly. The extent to which this happens is a proxy for bias expressed as uncertainty in adecision-making context. Our measure's main advantage is that it does not depend on any machine learning prediction model but adistance function. In this paper, we extend our study by exploring the existence of bias encoded implicitly in non-protected featuresas defined by the correlation between protected and unprotected attributes. This analysis leads to four scenarios that domain experts should evaluate before deciding how to tackle bias. In addition, we conduct a sensitivity analysis to determine the fuzzy operatorsand distance function that best capture change in the boundary regions.