Linear Precoding Design for OTFS Systems in Time/Frequency Selective Fading Channels

Even orthogonal time frequency space (OTFS) has been shown as a promising modulation scheme for high mobility doubly-selective fading channels, its attainability of full diversity order in either time or frequency selective fading channels has not been clarified. By performing pairwise error probability (PEP) analysis, we observe that the original OTFS system can not always guarantee full exploitation of the embedded diversity in either time or frequency selective fading channels. To address this issue and further improve system performance, this work proposes linear precoding solutions based on algebraic number theory for OTFS systems over time and frequency selective fading channels, respectively. The proposed linear precoded OTFS systems can guarantee the maximal diversity and potential coding gains in time/frequency selective fading channels without any transmission rate loss and do not require the channel state information (CSI) at the transmitter. Simulation results are finally provided to illustrate the superiority of our proposed precoded OTFS over both the original unprecoded and the existing phase rotation OTFS systems in time/frequency selective fading channels.

New Lower Bounds on Aperiodic Ambiguity Function of Unimodular Sequences

This paper presents new aperiodic ambiguity function (AF) lower bounds of unimodular sequences under certain low ambiguity zone. Our key idea, motivated by the Levenshtein correlation bound, is to introduce two weight vectors associated to the delay and Doppler shifts, respectively, and then exploit the upper and lower bounds on the Frobenius norm of the weighted auto- and cross-AF matrices to derive these bounds. Furthermore, the inherent structure properties of aperiodic AF are also utilized in our derivation. The derived bounds are useful design guidelines for optimal AF shaping in modern communication and radar systems.

Flag Sequence Set Design for Low-Complexity Delay-Doppler Estimation

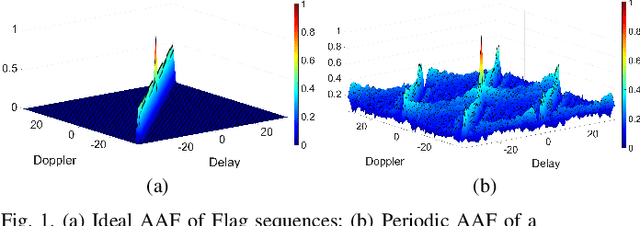
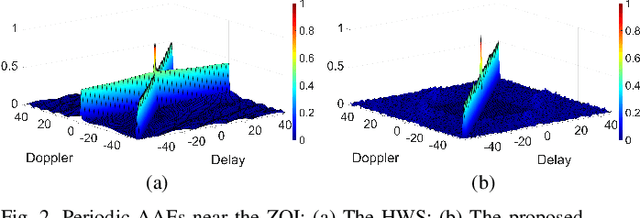
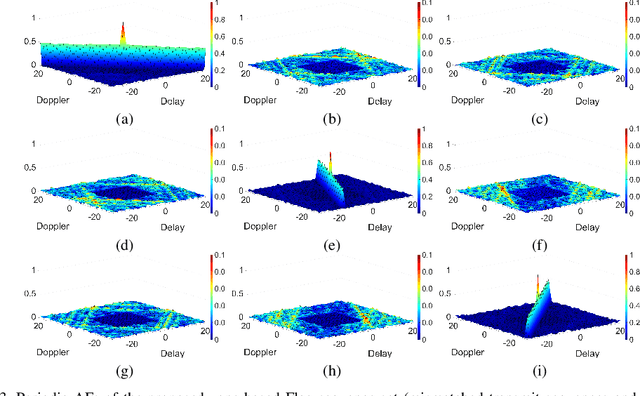
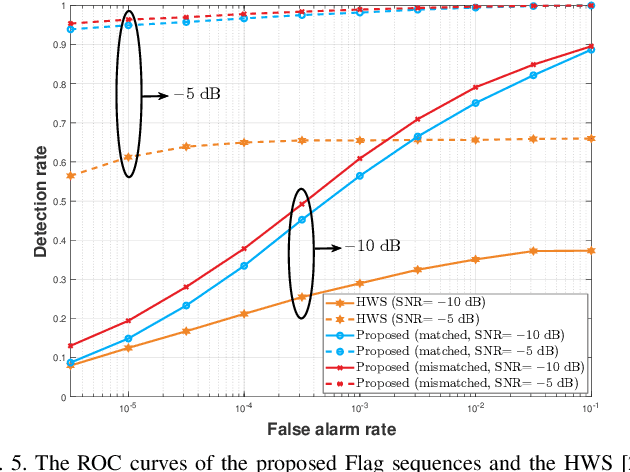
This paper studies Flag sequences for lowcomplexity delay-Doppler estimation by exploiting their distinctive peak-curtain ambiguity functions (AFs). Unlike the existing Flag sequence designs that are limited to prime lengths and periodic auto-AFs, we aim to design Flag sequence sets of arbitrary lengths and with low (nontrivial) periodic/aperiodic auto- and cross-AFs. Since every Flag sequence consists of a Curtain sequence and a Peak sequence, we first investigate the algebraic design of zone-based Curtain sequence sets of arbitrary lengths. Our proposed design gives rise to novel Curtain sequence sets with ideal curtain auto-AFs and low/zero cross-AFs within the delay-Doppler zone of interest. Leveraging these Curtain sequence sets, two optimization problems are formulated to minimize the summed customized weighted integrated sidelobe level (SCWISL) of the Flag sequence set. Accelerated Parallel Partially Majorization-Minimization Algorithms are proposed to jointly optimize the transmit Flag sequences and matched/mismatched reference sequences stored in the receiver. Simulations demonstrate that our proposed Flag sequences lead to improved SCWISL and customized peak-to-max-sidelobe ratio compared with the existing Flag sequences. Additionally, our Flag sequences under Flag method exhibit Mean Squared Errors that approach the Cramer-Rao Lower Bound and the Sampling Bound at high signal-to-noise power ratios.