FastHyMix: Fast and Parameter-free Hyperspectral Image Mixed Noise Removal

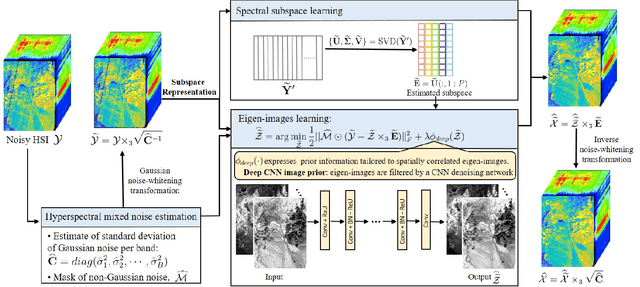
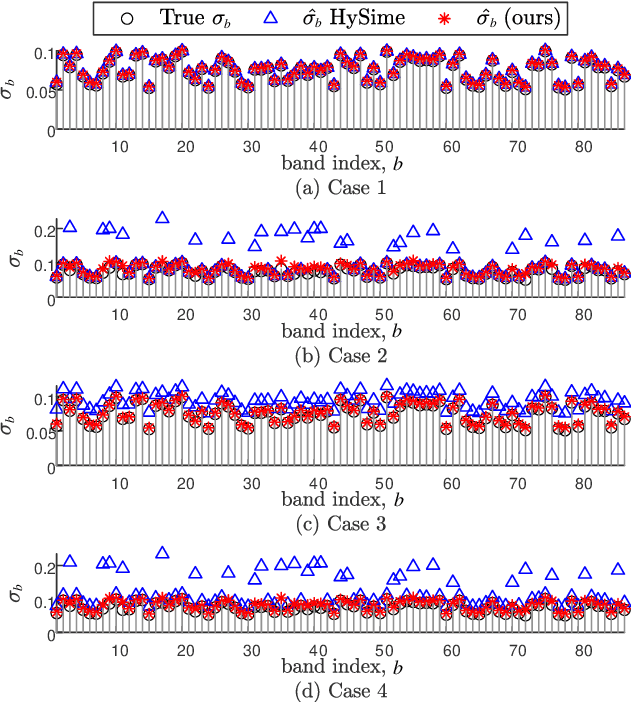
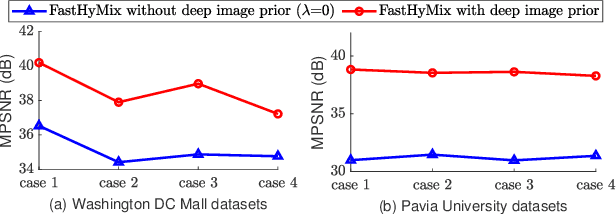
Hyperspectral imaging with high spectral resolution plays an important role in finding objects, identifying materials, or detecting processes. The decrease of the widths of spectral bands leads to a decrease in the signal-to-noise ratio (SNR) of measurements. The decreased SNR reduces the reliability of measured features or information extracted from HSIs. Furthermore, the image degradations linked with various mechanisms also result in different types of noise, such as Gaussian noise, impulse noise, deadlines, and stripes. This paper introduces a fast and parameter-free hyperspectral image mixed noise removal method (termed FastHyMix), which characterizes the complex distribution of mixed noise by using a Gaussian mixture model and exploits two main characteristics of hyperspectral data, namely low-rankness in the spectral domain and high correlation in the spatial domain. The Gaussian mixture model enables us to make a good estimation of Gaussian noise intensity and the location of sparse noise. The proposed method takes advantage of the low-rankness using subspace representation and the spatial correlation of HSIs by adding a powerful deep image prior, which is extracted from a neural denoising network. An exhaustive array of experiments and comparisons with state-of-the-art denoisers were carried out. The experimental results show significant improvement in both synthetic and real datasets. A MATLAB demo of this work will be available at https://github.com/LinaZhuang for the sake of reproducibility.

Using Low-rank Representation of Abundance Maps and Nonnegative Tensor Factorization for Hyperspectral Nonlinear Unmixing

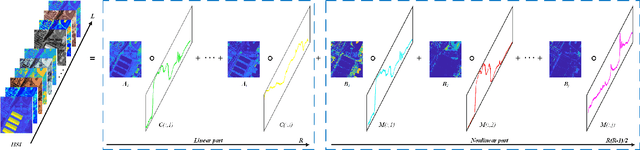
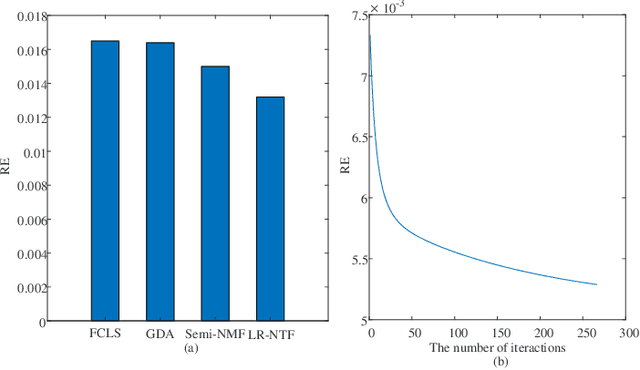
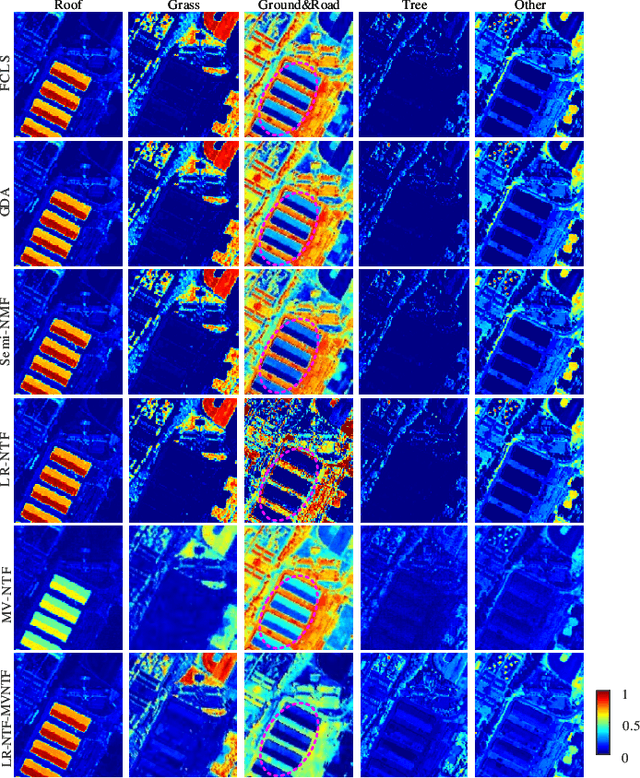
Tensor-based methods have been widely studied to attack inverse problems in hyperspectral imaging since a hyperspectral image (HSI) cube can be naturally represented as a third-order tensor, which can perfectly retain the spatial information in the image. In this article, we extend the linear tensor method to the nonlinear tensor method and propose a nonlinear low-rank tensor unmixing algorithm to solve the generalized bilinear model (GBM). Specifically, the linear and nonlinear parts of the GBM can both be expressed as tensors. Furthermore, the low-rank structures of abundance maps and nonlinear interaction abundance maps are exploited by minimizing their nuclear norm, thus taking full advantage of the high spatial correlation in HSIs. Synthetic and real-data experiments show that the low rank of abundance maps and nonlinear interaction abundance maps exploited in our method can improve the performance of the nonlinear unmixing. A MATLAB demo of this work will be available at https://github.com/LinaZhuang for the sake of reproducibility.

Hyperspectral Image Denoising and Anomaly Detection Based on Low-rank and Sparse Representations

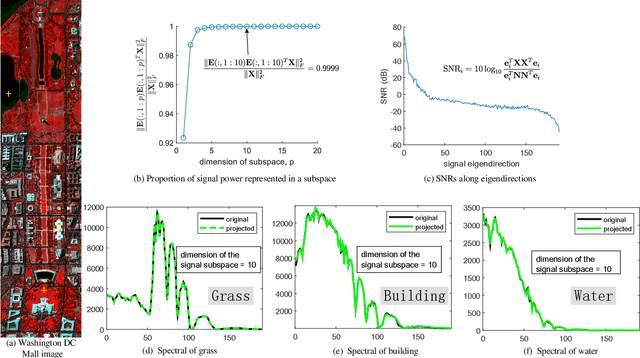
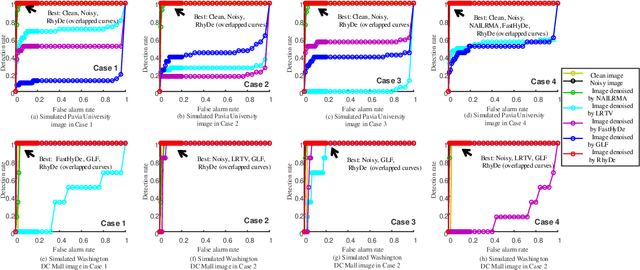
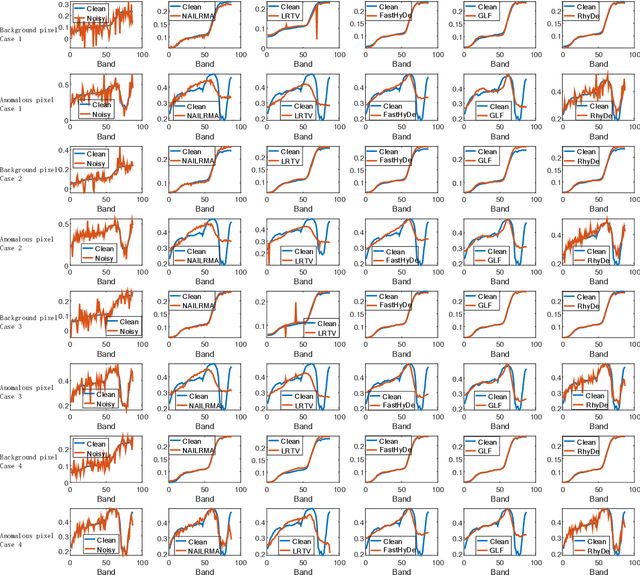
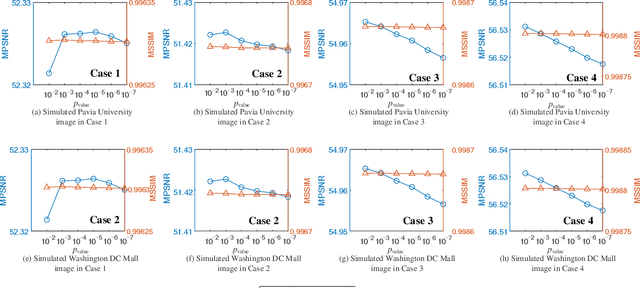
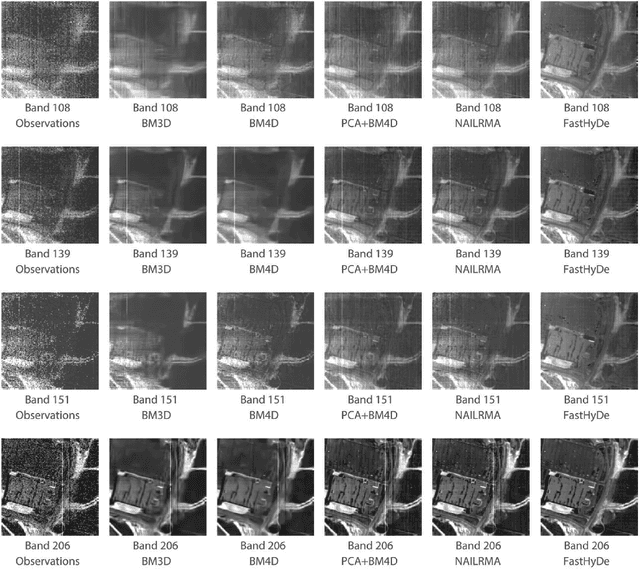
Hyperspectral imaging measures the amount of electromagnetic energy across the instantaneous field of view at a very high resolution in hundreds or thousands of spectral channels. This enables objects to be detected and the identification of materials that have subtle differences between them. However, the increase in spectral resolution often means that there is a decrease in the number of photons received in each channel, which means that the noise linked to the image formation process is greater. This degradation limits the quality of the extracted information and its potential applications. Thus, denoising is a fundamental problem in hyperspectral image (HSI) processing. As images of natural scenes with highly correlated spectral channels, HSIs are characterized by a high level of self-similarity and can be well approximated by low-rank representations. These characteristics underlie the state-of-the-art methods used in HSI denoising. However, where there are rarely occurring pixel types, the denoising performance of these methods is not optimal, and the subsequent detection of these pixels may be compromised. To address these hurdles, in this article, we introduce RhyDe (Robust hyperspectral Denoising), a powerful HSI denoiser, which implements explicit low-rank representation, promotes self-similarity, and, by using a form of collaborative sparsity, preserves rare pixels. The denoising and detection effectiveness of the proposed robust HSI denoiser is illustrated using semireal and real data.

Fast Hyperspectral Image Denoising and Inpainting Based on Low-Rank and Sparse Representations

This paper introduces two very fast and competitive hyperspectral image (HSI) restoration algorithms: fast hyperspectral denoising (FastHyDe), a denoising algorithm able to cope with Gaussian and Poissonian noise, and fast hyperspectral inpainting (FastHyIn), an inpainting algorithm to restore HSIs where some observations from known pixels in some known bands are missing. FastHyDe and FastHyIn fully exploit extremely compact and sparse HSI representations linked with their low-rank and self-similarity characteristics. In a series of experiments with simulated and real data, the newly introduced FastHyDe and FastHyIn compete with the state-of-the-art methods, with much lower computational complexity.