Liangyuan Hu
A flexible Bayesian g-formula for causal survival analyses with time-dependent confounding
Feb 04, 2024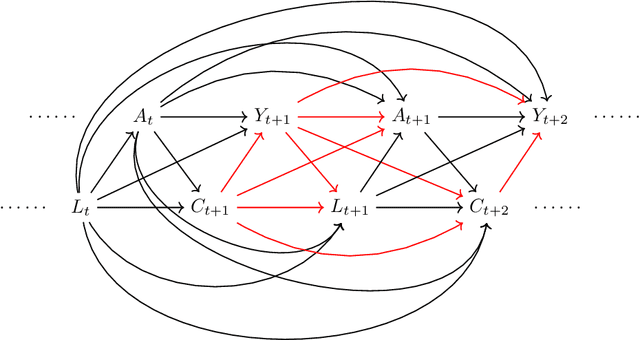
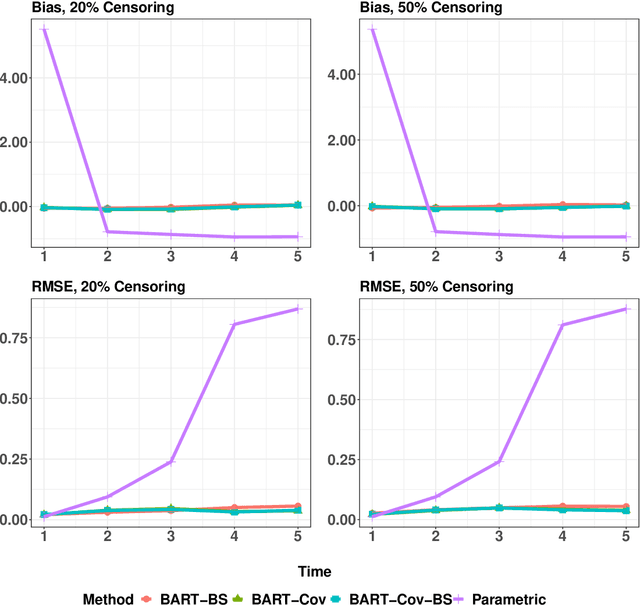
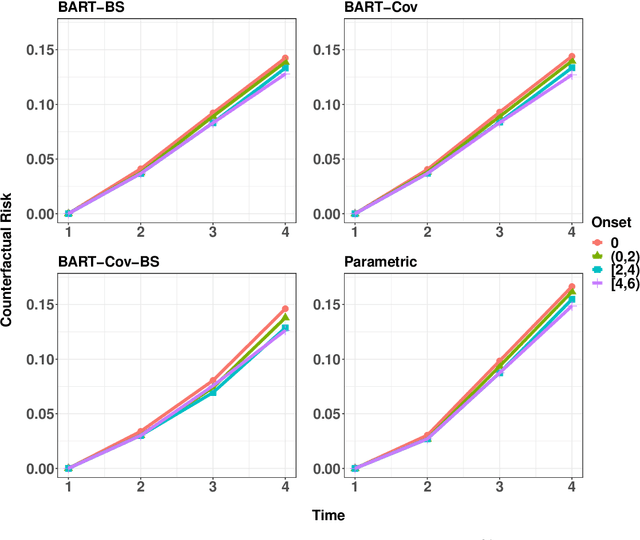
Abstract:In longitudinal observational studies with a time-to-event outcome, a common objective in causal analysis is to estimate the causal survival curve under hypothetical intervention scenarios within the study cohort. The g-formula is a particularly useful tool for this analysis. To enhance the traditional parametric g-formula approach, we developed a more adaptable Bayesian g-formula estimator. This estimator facilitates both longitudinal predictive and causal inference. It incorporates Bayesian additive regression trees in the modeling of the time-evolving generative components, aiming to mitigate bias due to model misspecification. Specifically, we introduce a more general class of g-formulas for discrete survival data. These formulas can incorporate the longitudinal balancing scores, which serve as an effective method for dimension reduction and are vital when dealing with an expanding array of time-varying confounders. The minimum sufficient formulation of these longitudinal balancing scores is linked to the nature of treatment regimes, whether static or dynamic. For each type of treatment regime, we provide posterior sampling algorithms, which are grounded in the Bayesian additive regression trees framework. We have conducted simulation studies to illustrate the empirical performance of our proposed Bayesian g-formula estimators, and to compare them with existing parametric estimators. We further demonstrate the practical utility of our methods in real-world scenarios using data from the Yale New Haven Health System's electronic health records.
Variable selection with missing data in both covariates and outcomes: Imputation and machine learning
Apr 06, 2021
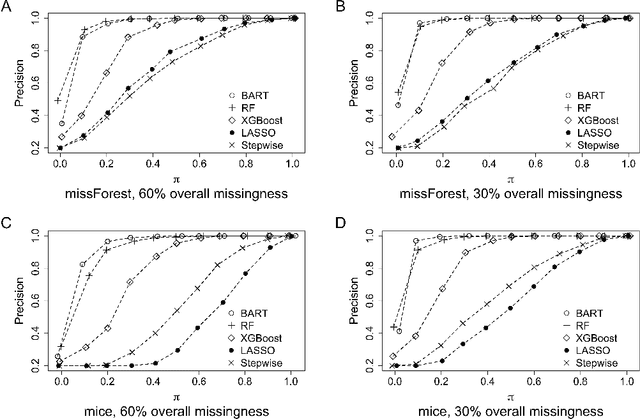


Abstract:The missing data issue is ubiquitous in health studies. Variable selection in the presence of both missing covariates and outcomes is an important statistical research topic but has been less studied. Existing literature focuses on parametric regression techniques that provide direct parameter estimates of the regression model. In practice, parametric regression models are often sub-optimal for variable selection because they are susceptible to misspecification. Machine learning methods considerably weaken the parametric assumptions and increase modeling flexibility, but do not provide as naturally defined variable importance measure as the covariate effect native to parametric models. We investigate a general variable selection approach when both the covariates and outcomes can be missing at random and have general missing data patterns. This approach exploits the flexibility of machine learning modeling techniques and bootstrap imputation, which is amenable to nonparametric methods in which the covariate effects are not directly available. We conduct expansive simulations investigating the practical operating characteristics of the proposed variable selection approach, when combined with four tree-based machine learning methods, XGBoost, Random Forests, Bayesian Additive Regression Trees (BART) and Conditional Random Forests, and two commonly used parametric methods, lasso and backward stepwise selection. Numeric results show XGBoost and BART have the overall best performance across various settings. Guidance for choosing methods appropriate to the structure of the analysis data at hand are discussed. We further demonstrate the methods via a case study of risk factors for 3-year incidence of metabolic syndrome with data from the Study of Women's Health Across the Nation.
Estimation of causal effects of multiple treatments in healthcare database studies with rare outcomes
Aug 18, 2020

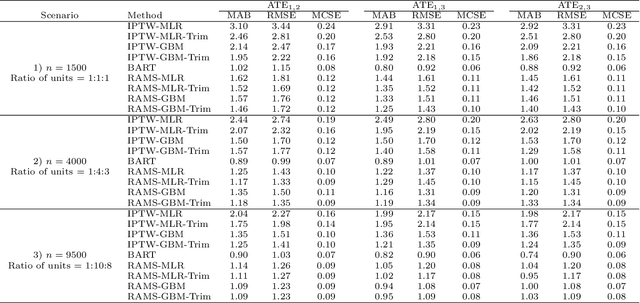
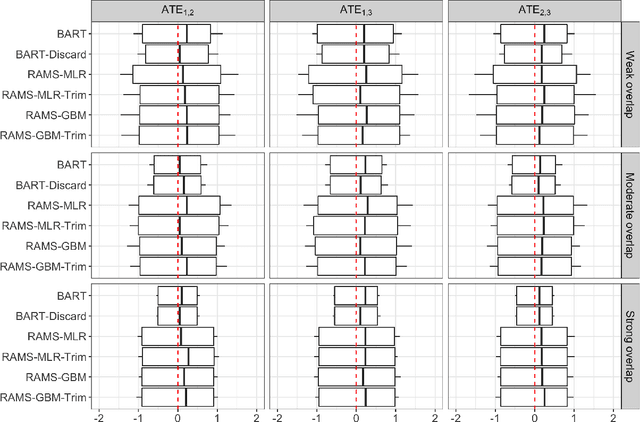
Abstract:The preponderance of large-scale healthcare databases provide abundant opportunities for comparative effectiveness research. Evidence necessary to making informed treatment decisions often relies on comparing effectiveness of multiple treatment options on outcomes of interest observed in a small number of individuals. Causal inference with multiple treatments and rare outcomes is a subject that has been treated sparingly in the literature. This paper designs three sets of simulations, representative of the structure of our healthcare database study, and propose causal analysis strategies for such settings. We investigate and compare the operating characteristics of three types of methods and their variants: Bayesian Additive Regression Trees (BART), regression adjustment on multivariate spline of generalized propensity scores (RAMS) and inverse probability of treatment weighting (IPTW) with multinomial logistic regression or generalized boosted models. Our results suggest that BART and RAMS provide lower bias and mean squared error, and the widely used IPTW methods deliver unfavorable operating characteristics. We illustrate the methods using a case study evaluating the comparative effectiveness of robotic-assisted surgery, video-assisted thoracoscopic surgery and open thoracotomy for treating non-small cell lung cancer.
Estimating Heterogeneous Survival Treatment Effect via Machine/Deep Learning Methods in Observational Studies
Aug 17, 2020
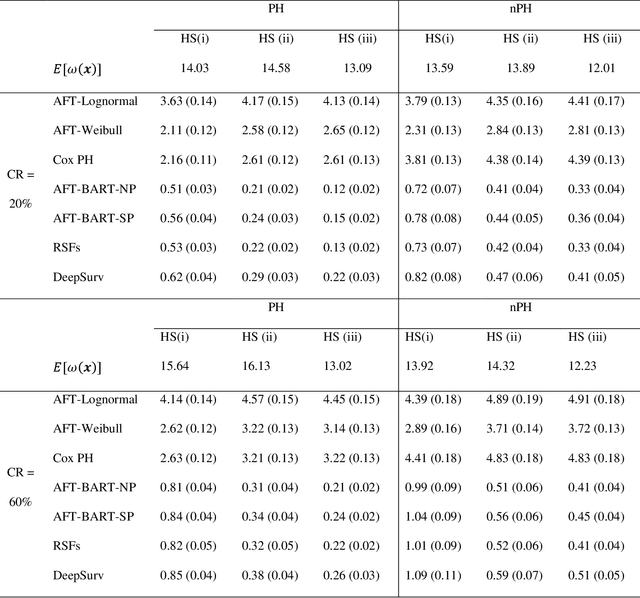
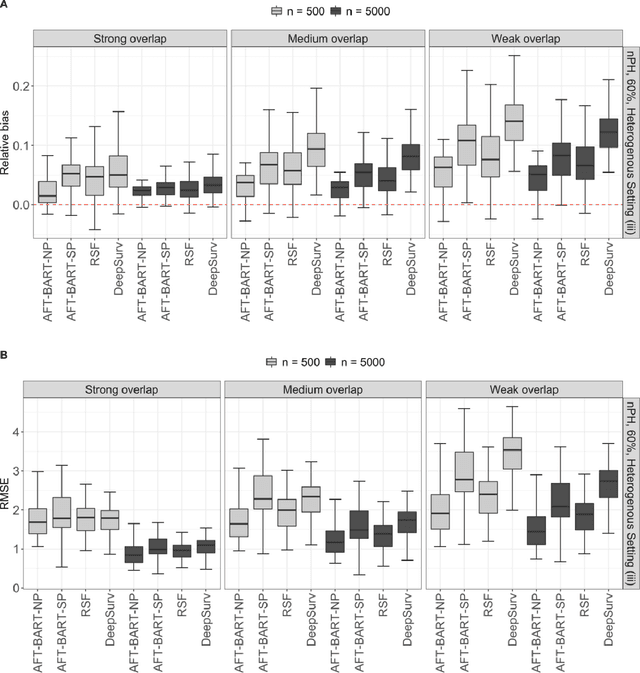
Abstract:The rise of personalized medicine necessitates improved causal inference methods for detecting treatment effect heterogeneity (TEH). Approaches for estimating TEH with observational data have largely focused on continuous outcomes. Methods for estimating TEH with right-censored survival outcomes are relatively limited and have been less vetted. Using flexible machine/deep learning (ML/DL) methods within the counterfactual framework is a promising approach to address challenges due to complex individual characteristics, to which treatments need to be tailored. We contribute a series of simulations representing a variety of confounded heterogenous survival treatment effect settings with varying degrees of covariate overlap, and compare the operating characteristics of three state-of-the-art survival ML/DL methods for the estimation of TEH. Our results show that the nonparametric Bayesian Additive Regression Trees within the framework of accelerated failure time model (AFT-BART-NP) consistently has the best performance, in terms of both bias and root-mean-squared-error. Additionally, AFT-BART-NP could provide nominal confidence interval coverage when covariate overlap is moderate or strong. Under lack of overlap where accurate estimation of the average causal effect is generally challenging, AFT-BART-NP still provides valid point and interval estimates for the treatment effect among units near the centroid of the propensity score distribution.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge