Progressive-X+: Clustering in the Consensus Space

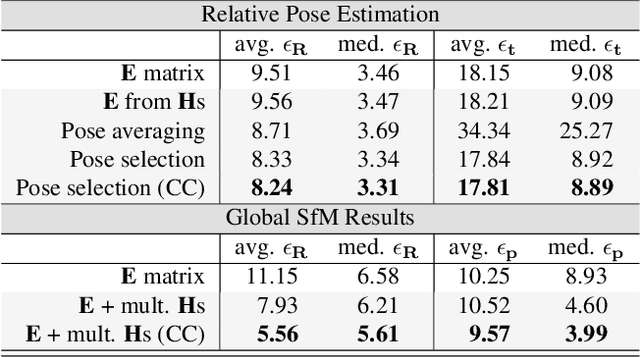
We propose Progressive-X+, a new algorithm for finding an unknown number of geometric models, e.g., homographies. The problem is formalized as finding dominant model instances progressively without forming crisp point-to-model assignments. Dominant instances are found via RANSAC-like sampling and a consolidation process driven by a model quality function considering previously proposed instances. New ones are found by clustering in the consensus space. This new formulation leads to a simple iterative algorithm with state-of-the-art accuracy while running in real-time on a number of vision problems. Also, we propose a sampler reflecting the fact that real-world data tend to form spatially coherent structures. The sampler returns connected components in a progressively growing neighborhood-graph. We present a number of applications where the use of multiple geometric models improves accuracy. These include using multiple homographies to estimate relative poses for global SfM; pose estimation from generalized homographies; and trajectory estimation of fast-moving objects.

Pose Estimation for Vehicle-mounted Cameras via Horizontal and Vertical Planes

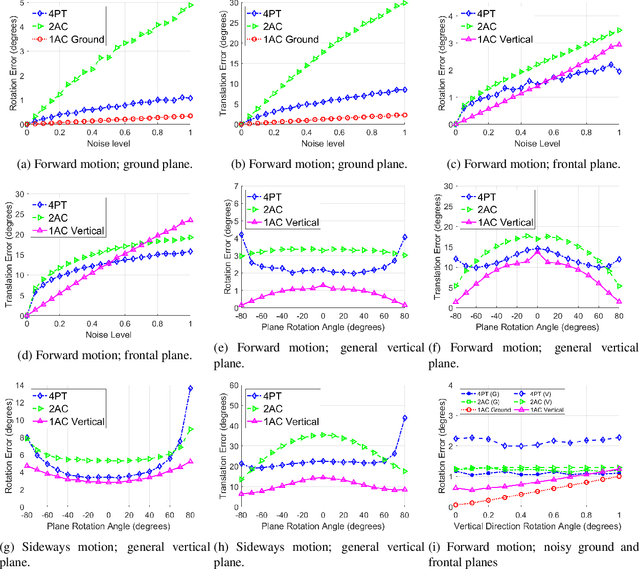
We propose two novel solvers for estimating the egomotion of a calibrated camera mounted to a moving vehicle from a single affine correspondence via recovering special homographies. For the first class of solvers, the sought plane is expected to be perpendicular to one of the camera axes. For the second class, the plane is orthogonal to the ground with unknown normal, e.g., it is a building facade. Both methods are solved via a linear system with a small coefficient matrix, thus, being extremely efficient. Both the minimal and over-determined cases can be solved by the proposed methods. They are tested on synthetic data and on publicly available real-world datasets. The novel methods are more accurate or comparable to the traditional algorithms and are faster when included in state of the art robust estimators.

Automatic Estimation of Sphere Centers from Images of Calibrated Cameras

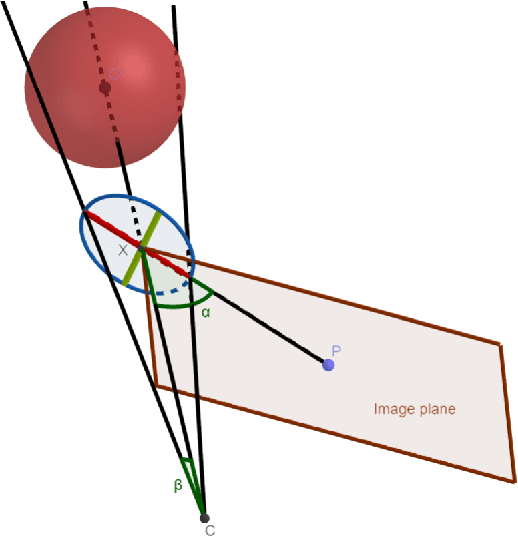
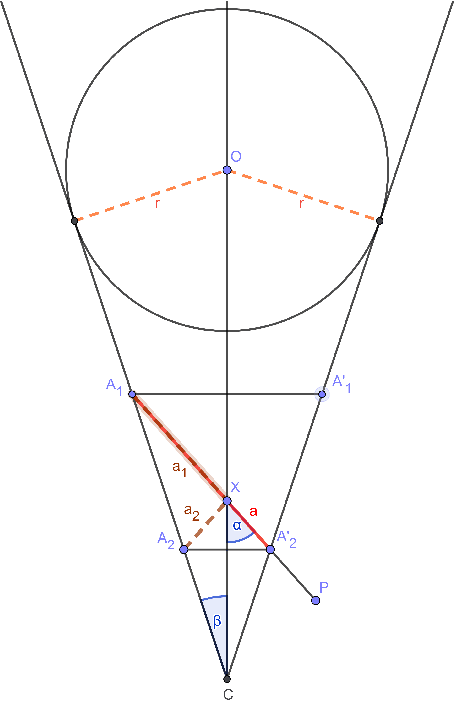
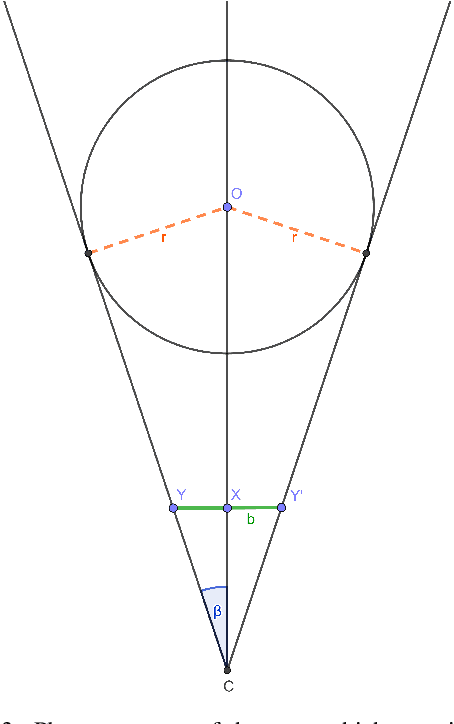
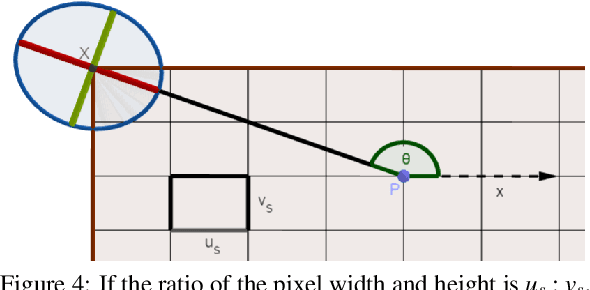
Calibration of devices with different modalities is a key problem in robotic vision. Regular spatial objects, such as planes, are frequently used for this task. This paper deals with the automatic detection of ellipses in camera images, as well as to estimate the 3D position of the spheres corresponding to the detected 2D ellipses. We propose two novel methods to (i) detect an ellipse in camera images and (ii) estimate the spatial location of the corresponding sphere if its size is known. The algorithms are tested both quantitatively and qualitatively. They are applied for calibrating the sensor system of autonomous cars equipped with digital cameras, depth sensors and LiDAR devices.

Relative planar motion for vehicle-mounted cameras from a single affine correspondence

Two solvers are proposed for estimating the extrinsic camera parameters from a single affine correspondence assuming general planar motion. In this case, the camera movement is constrained to a plane and the image plane is orthogonal to the ground. The algorithms do not assume other constraints, e.g.\ the non-holonomic one, to hold. A new minimal solver is proposed for the semi-calibrated case, i.e. the camera parameters are known except a common focal length. Another method is proposed for the fully calibrated case. Due to requiring a single correspondence, robust estimation, e.g. histogram voting, leads to a fast and accurate procedure. The proposed methods are tested in our synthetic environment and on publicly available real datasets consisting of videos through tens of kilometres. They are superior to the state-of-the-art both in terms of accuracy and processing time.

Least-squares Optimal Relative Planar Motion for Vehicle-mounted Cameras

A new closed-form solver is proposed minimizing the algebraic error optimally, in the least-squares sense, to estimate the relative planar motion of two calibrated cameras. The main objective is to solve the over-determined case, i.e., when a larger-than-minimal sample of point correspondences is given - thus, estimating the motion from at least three correspondences. The algorithm requires the camera movement to be constrained to a plane, e.g. mounted to a vehicle, and the image plane to be orthogonal to the ground. The solver obtains the motion parameters as the roots of a 6-th degree polynomial. It is validated both in synthetic experiments and on publicly available real-world datasets that using the proposed solver leads to results superior to the state-of-the-art in terms of geometric accuracy with no noticeable deterioration in the processing time.

A Minimal Solution for Two-view Focal-length Estimation using Two Affine Correspondences

A minimal solution using two affine correspondences is presented to estimate the common focal length and the fundamental matrix between two semi-calibrated cameras - known intrinsic parameters except a common focal length. To the best of our knowledge, this problem is unsolved. The proposed approach extends point correspondence-based techniques with linear constraints derived from local affine transformations. The obtained multivariate polynomial system is efficiently solved by the hidden-variable technique. Observing the geometry of local affinities, we introduce novel conditions eliminating invalid roots. To select the best one out of the remaining candidates, a root selection technique is proposed outperforming the recent ones especially in case of high-level noise. The proposed 2-point algorithm is validated on both synthetic data and 104 publicly available real image pairs. A Matlab implementation of the proposed solution is included in the paper.