Encoderless Gimbal Calibration of Dynamic Multi-Camera Clusters

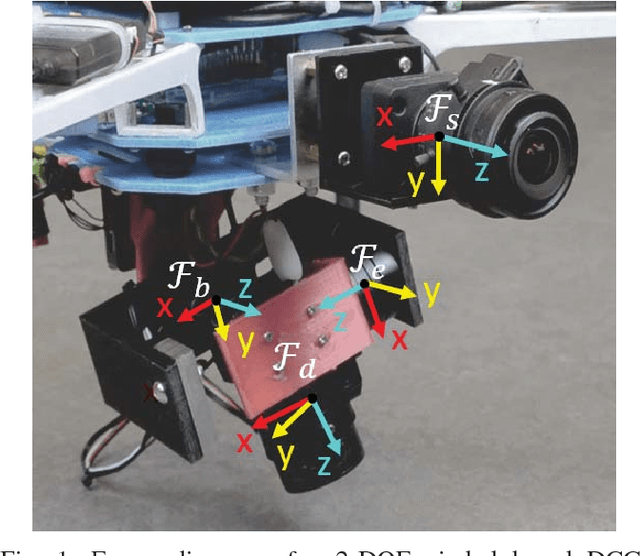
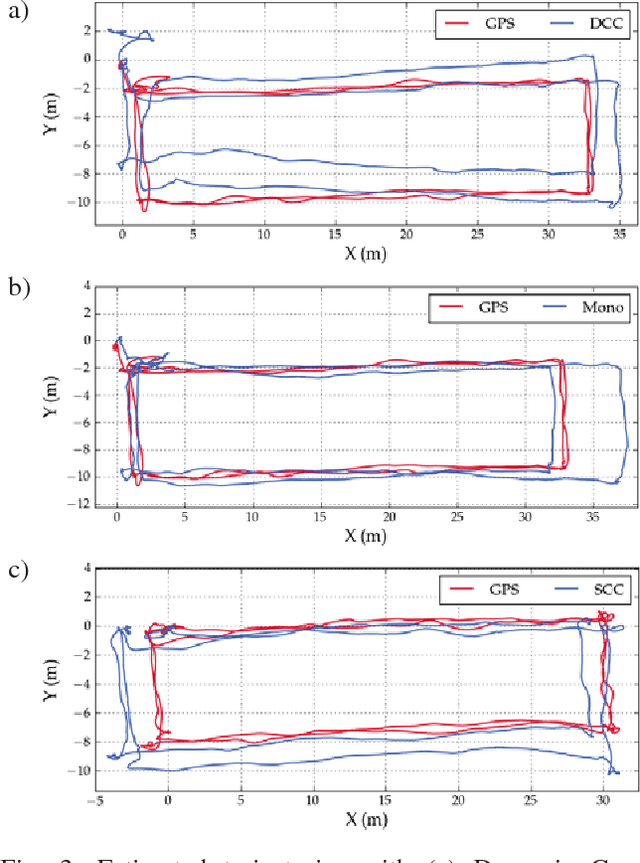
Dynamic Camera Clusters (DCCs) are multi-camera systems where one or more cameras are mounted on actuated mechanisms such as a gimbal. Existing methods for DCC calibration rely on joint angle measurements to resolve the time-varying transformation between the dynamic and static camera. This information is usually provided by motor encoders, however, joint angle measurements are not always readily available on off-the-shelf mechanisms. In this paper, we present an encoderless approach for DCC calibration which simultaneously estimates the kinematic parameters of the transformation chain as well as the unknown joint angles. We also demonstrate the integration of an encoderless gimbal mechanism with a state-of-the art VIO algorithm, and show the extensions required in order to perform simultaneous online estimation of the joint angles and vehicle localization state. The proposed calibration approach is validated both in simulation and on a physical DCC composed of a 2-DOF gimbal mounted on a UAV. Finally, we show the experimental results of the calibrated mechanism integrated into the OKVIS VIO package, and demonstrate successful online joint angle estimation while maintaining localization accuracy that is comparable to a standard static multi-camera configuration.

Manifold Geometry with Fast Automatic Derivatives and Coordinate Frame Semantics Checking in C++

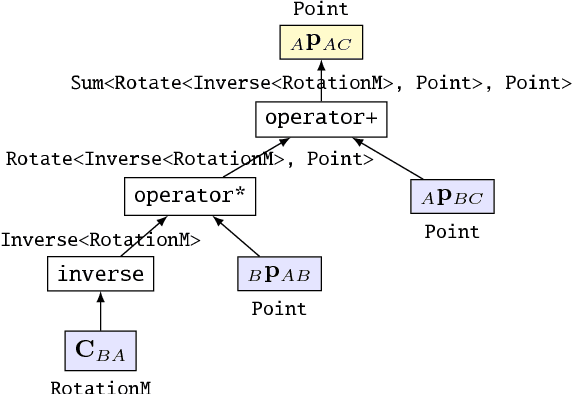
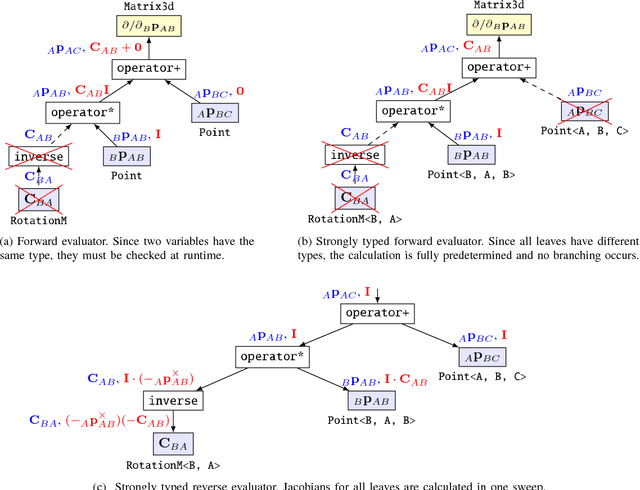
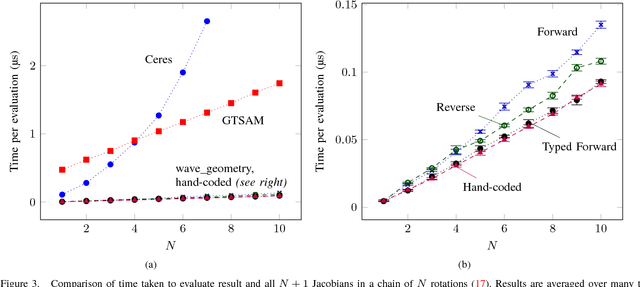
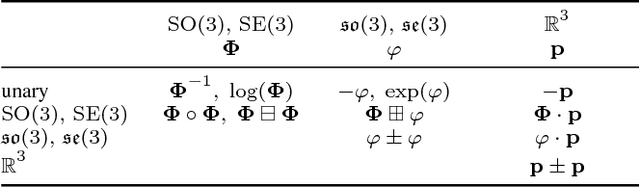
Computer vision and robotics problems often require representation and estimation of poses on the SE(3) manifold. Developers of algorithms that must run in real time face several time-consuming programming tasks, including deriving and computing analytic derivatives and avoiding mathematical errors when handling poses in multiple coordinate frames. To support rapid and error-free development, we present wave_geometry, a C++ manifold geometry library with two key contributions: expression template-based automatic differentiation and compile-time enforcement of coordinate frame semantics. We contrast the library with existing open source packages and show that it can evaluate Jacobians in forward and reverse mode with little to no runtime overhead compared to hand-coded derivatives. The library is available at https://github.com/wavelab/wave_geometry .