Faster Convergence for Transformer Fine-tuning with Line Search Methods

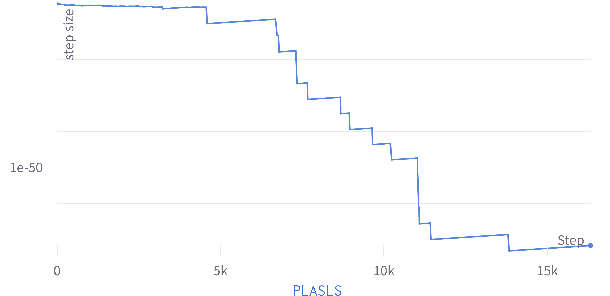
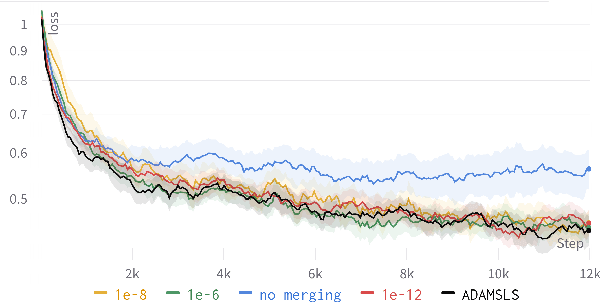
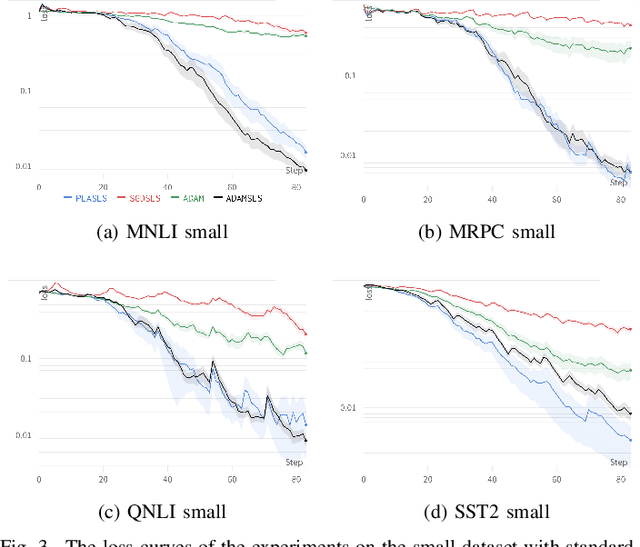
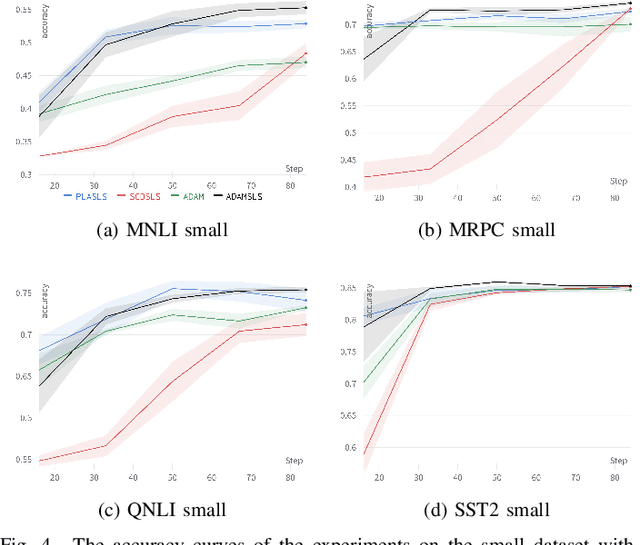
Recent works have shown that line search methods greatly increase performance of traditional stochastic gradient descent methods on a variety of datasets and architectures [1], [2]. In this work we succeed in extending line search methods to the novel and highly popular Transformer architecture and dataset domains in natural language processing. More specifically, we combine the Armijo line search with the Adam optimizer and extend it by subdividing the networks architecture into sensible units and perform the line search separately on these local units. Our optimization method outperforms the traditional Adam optimizer and achieves significant performance improvements for small data sets or small training budgets, while performing equal or better for other tested cases. Our work is publicly available as a python package, which provides a hyperparameter-free pytorch optimizer that is compatible with arbitrary network architectures.

Don't be so Monotone: Relaxing Stochastic Line Search in Over-Parameterized Models

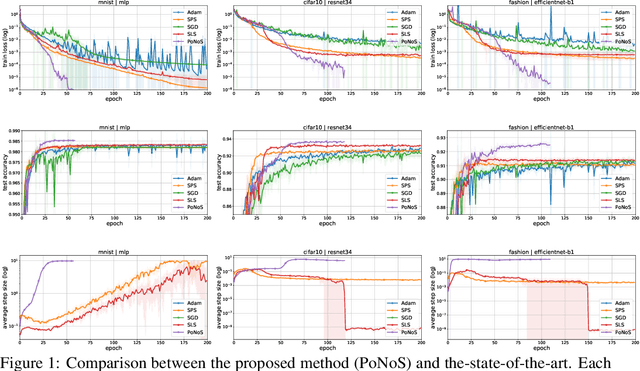
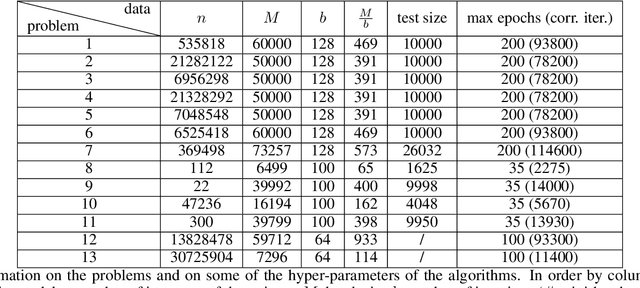
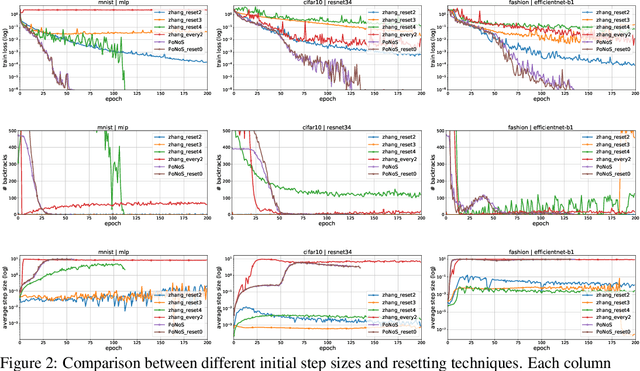
Recent works have shown that line search methods can speed up Stochastic Gradient Descent (SGD) and Adam in modern over-parameterized settings. However, existing line searches may take steps that are smaller than necessary since they require a monotone decrease of the (mini-)batch objective function. We explore nonmonotone line search methods to relax this condition and possibly accept larger step sizes. Despite the lack of a monotonic decrease, we prove the same fast rates of convergence as in the monotone case. Our experiments show that nonmonotone methods improve the speed of convergence and generalization properties of SGD/Adam even beyond the previous monotone line searches. We propose a POlyak NOnmonotone Stochastic (PoNoS) method, obtained by combining a nonmonotone line search with a Polyak initial step size. Furthermore, we develop a new resetting technique that in the majority of the iterations reduces the amount of backtracks to zero while still maintaining a large initial step size. To the best of our knowledge, a first runtime comparison shows that the epoch-wise advantage of line-search-based methods gets reflected in the overall computational time.