There is more to graphs than meets the eye: Learning universal features with self-supervision

We study the problem of learning universal features across multiple graphs through self-supervision. Graph self supervised learning has been shown to facilitate representation learning, and produce competitive models compared to supervised baselines. However, existing methods of self-supervision learn features from one graph, and thus, produce models that are specialized to a particular graph. We hypothesize that leveraging multiple graphs of the same type/class can improve the quality of learnt representations in the model by extracting features that are universal to the class of graphs. We adopt a transformer backbone that acts as a universal representation learning module for multiple graphs. We leverage neighborhood aggregation coupled with graph-specific embedding generator to transform disparate node embeddings from multiple graphs to a common space for the universal backbone. We learn both universal and graph-specific parameters in an end-to-end manner. Our experiments reveal that leveraging multiple graphs of the same type -- citation networks -- improves the quality of representations and results in better performance on downstream node classification task compared to self-supervision with one graph. The results of our study improve the state-of-the-art in graph self-supervised learning, and bridge the gap between self-supervised and supervised performance.

Uncertainty-aware deep learning for digital twin-driven monitoring: Application to fault detection in power lines

Deep neural networks (DNNs) are often coupled with physics-based models or data-driven surrogate models to perform fault detection and health monitoring of systems in the low data regime. These models serve as digital twins to generate large quantities of data to train DNNs which would otherwise be difficult to obtain from the real-life system. However, such models can exhibit parametric uncertainty that propagates to the generated data. In addition, DNNs exhibit uncertainty in the parameters learnt during training. In such a scenario, the performance of the DNN model will be influenced by the uncertainty in the physics-based model as well as the parameters of the DNN. In this article, we quantify the impact of both these sources of uncertainty on the performance of the DNN. We perform explicit propagation of uncertainty in input data through all layers of the DNN, as well as implicit prediction of output uncertainty to capture the former. Furthermore, we adopt Monte Carlo dropout to capture uncertainty in DNN parameters. We demonstrate the approach for fault detection of power lines with a physics-based model, two types of input data and three different neural network architectures. We compare the performance of such uncertainty-aware probabilistic models with their deterministic counterparts. The results show that the probabilistic models provide important information regarding the confidence of predictions, while also delivering an improvement in performance over deterministic models.

Object detection-based inspection of power line insulators: Incipient fault detection in the low data-regime

Deep learning-based object detection is a powerful approach for detecting faulty insulators in power lines. This involves training an object detection model from scratch, or fine tuning a model that is pre-trained on benchmark computer vision datasets. This approach works well with a large number of insulator images, but can result in unreliable models in the low data regime. The current literature mainly focuses on detecting the presence or absence of insulator caps, which is a relatively easy detection task, and does not consider detection of finer faults such as flashed and broken disks. In this article, we formulate three object detection tasks for insulator and asset inspection from aerial images, focusing on incipient faults in disks. We curate a large reference dataset of insulator images that can be used to learn robust features for detecting healthy and faulty insulators. We study the advantage of using this dataset in the low target data regime by pre-training on the reference dataset followed by fine-tuning on the target dataset. The results suggest that object detection models can be used to detect faults in insulators at a much incipient stage, and that transfer learning adds value depending on the type of object detection model. We identify key factors that dictate performance in the low data-regime and outline potential approaches to improve the state-of-the-art.

Challenges and Opportunities in Deep Reinforcement Learning with Graph Neural Networks: A Comprehensive review of Algorithms and Applications

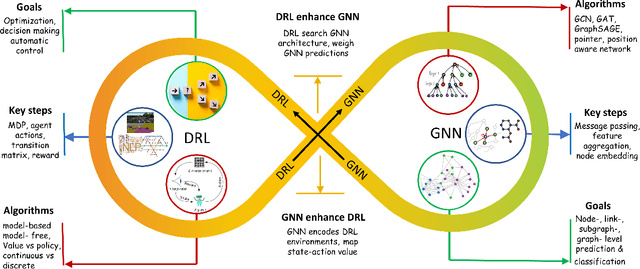
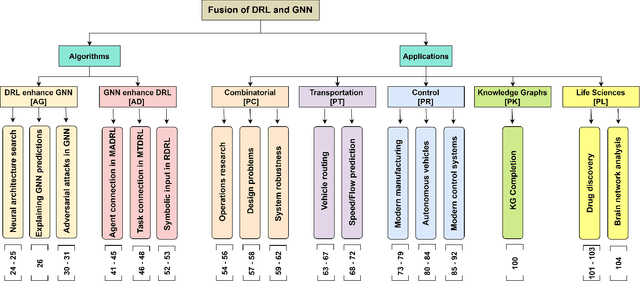
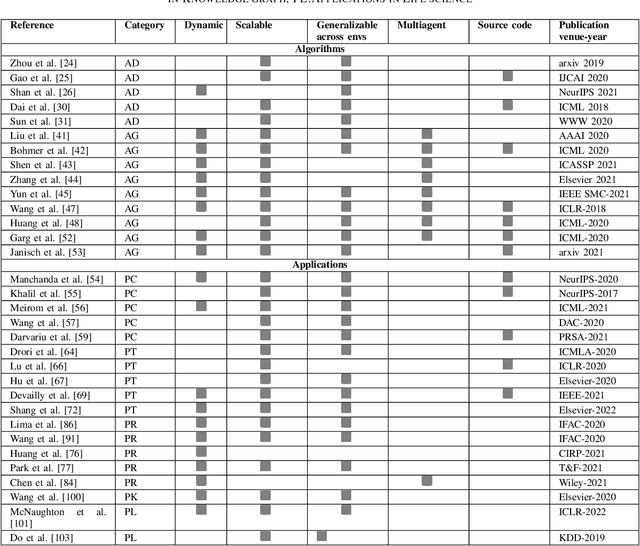
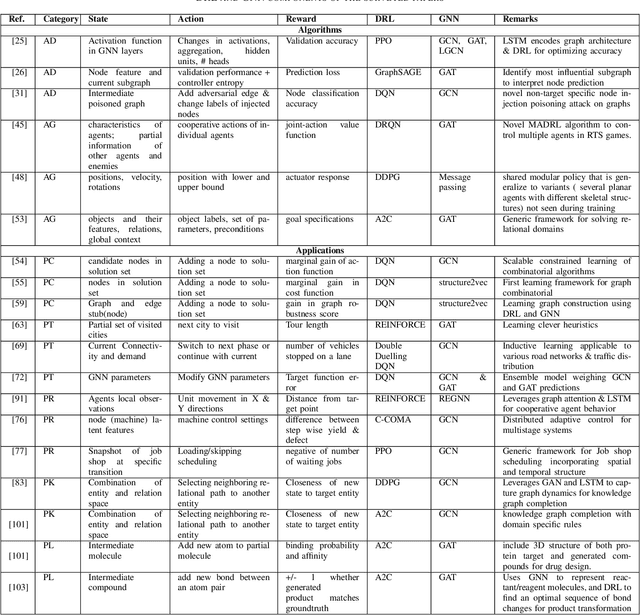
Deep reinforcement learning (DRL) has empowered a variety of artificial intelligence fields, including pattern recognition, robotics, recommendation-systems, and gaming. Similarly, graph neural networks (GNN) have also demonstrated their superior performance in supervised learning for graph-structured data. In recent times, the fusion of GNN with DRL for graph-structured environments has attracted a lot of attention. This paper provides a comprehensive review of these hybrid works. These works can be classified into two categories: (1) algorithmic enhancement, where DRL and GNN complement each other for better utility; (2) application-specific enhancement, where DRL and GNN support each other. This fusion effectively addresses various complex problems in engineering and life sciences. Based on the review, we further analyze the applicability and benefits of fusing these two domains, especially in terms of increasing generalizability and reducing computational complexity. Finally, the key challenges in integrating DRL and GNN, and potential future research directions are highlighted, which will be of interest to the broader machine learning community.

A General Framework for quantifying Aleatoric and Epistemic uncertainty in Graph Neural Networks

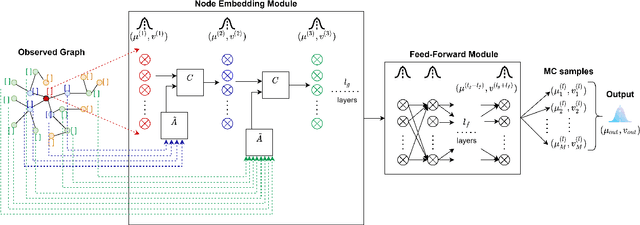
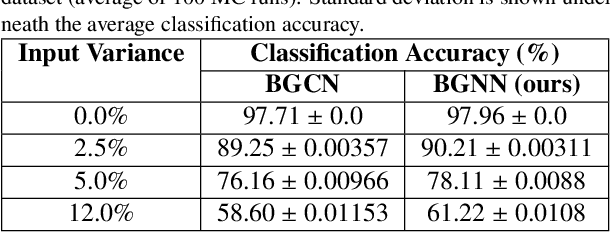
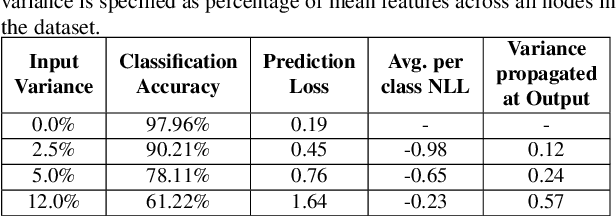
Graph Neural Networks (GNN) provide a powerful framework that elegantly integrates Graph theory with Machine learning for modeling and analysis of networked data. We consider the problem of quantifying the uncertainty in predictions of GNN stemming from modeling errors and measurement uncertainty. We consider aleatoric uncertainty in the form of probabilistic links and noise in feature vector of nodes, while epistemic uncertainty is incorporated via a probability distribution over the model parameters. We propose a unified approach to treat both sources of uncertainty in a Bayesian framework, where Assumed Density Filtering is used to quantify aleatoric uncertainty and Monte Carlo dropout captures uncertainty in model parameters. Finally, the two sources of uncertainty are aggregated to estimate the total uncertainty in predictions of a GNN. Results in the real-world datasets demonstrate that the Bayesian model performs at par with a frequentist model and provides additional information about predictions uncertainty that are sensitive to uncertainties in the data and model.

Graph neural network based approximation of Node Resiliency in complex networks

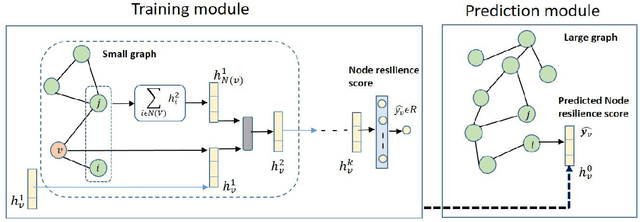
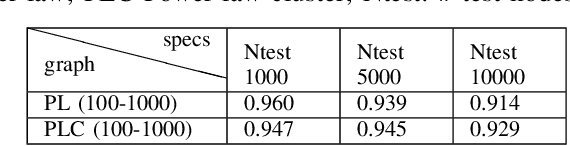
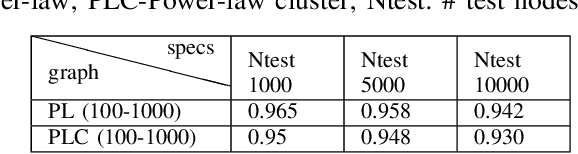
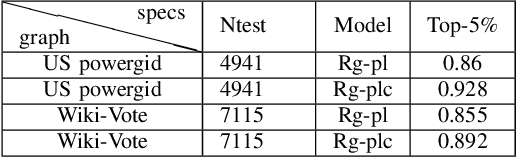
The emphasis on optimal operations and efficiency has led to increased complexity in engineered systems. This in turn increases the vulnerability of the system. However, with the increasing frequency of extreme events, resilience has now become an important consideration. Resilience quantifies the ability of the system to absorb and recover from extreme conditions. Graph theory is a widely used framework for modeling complex engineered systems to evaluate their resilience to attacks. Most existing methods in resilience analysis are based on an iterative approach that explores each node/link of a graph. These methods suffer from high computational complexity and the resulting analysis is network specific. To address these challenges, we propose a graph neural network (GNN) based framework for approximating node resilience in large complex networks. The proposed framework defines a GNN model that learns the node rank on a small representative subset of nodes. Then, the trained model can be employed to predict the ranks of unseen nodes in similar types of graphs. The scalability of the framework is demonstrated through the prediction of node ranks in real-world graphs. The proposed approach is accurate in approximating the node resilience scores and offers a significant computational advantage over conventional approaches.

Robust and Efficient Swarm Communication Topologies for Hostile Environments

Swarm Intelligence-based optimization techniques combine systematic exploration of the search space with information available from neighbors and rely strongly on communication among agents. These algorithms are typically employed to solve problems where the function landscape is not adequately known and there are multiple local optima that could result in premature convergence for other algorithms. Applications of such algorithms can be found in communication systems involving design of networks for efficient information dissemination to a target group, targeted drug-delivery where drug molecules search for the affected site before diffusing, and high-value target localization with a network of drones. In several of such applications, the agents face a hostile environment that can result in loss of agents during the search. Such a loss changes the communication topology of the agents and hence the information available to agents, ultimately influencing the performance of the algorithm. In this paper, we present a study of the impact of loss of agents on the performance of such algorithms as a function of the initial network configuration. We use particle swarm optimization to optimize an objective function with multiple sub-optimal regions in a hostile environment and study its performance for a range of network topologies with loss of agents. The results reveal interesting trade-offs between efficiency, robustness, and performance for different topologies that are subsequently leveraged to discover general properties of networks that maximize performance. Moreover, networks with small-world properties are seen to maximize performance under hostile conditions.