A General Framework for quantifying Aleatoric and Epistemic uncertainty in Graph Neural Networks
Paper and Code
May 20, 2022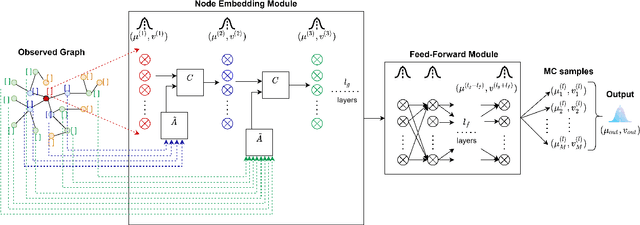
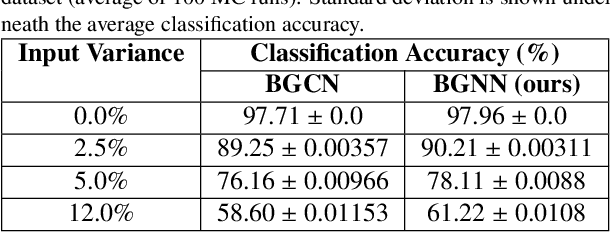
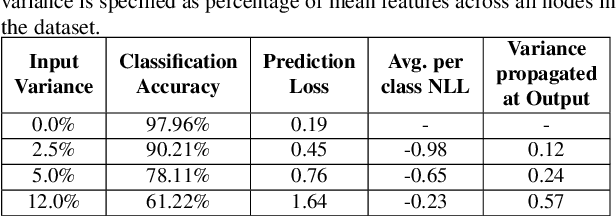
Graph Neural Networks (GNN) provide a powerful framework that elegantly integrates Graph theory with Machine learning for modeling and analysis of networked data. We consider the problem of quantifying the uncertainty in predictions of GNN stemming from modeling errors and measurement uncertainty. We consider aleatoric uncertainty in the form of probabilistic links and noise in feature vector of nodes, while epistemic uncertainty is incorporated via a probability distribution over the model parameters. We propose a unified approach to treat both sources of uncertainty in a Bayesian framework, where Assumed Density Filtering is used to quantify aleatoric uncertainty and Monte Carlo dropout captures uncertainty in model parameters. Finally, the two sources of uncertainty are aggregated to estimate the total uncertainty in predictions of a GNN. Results in the real-world datasets demonstrate that the Bayesian model performs at par with a frequentist model and provides additional information about predictions uncertainty that are sensitive to uncertainties in the data and model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge