Surveying the Effects of Quality, Diversity, and Complexity in Synthetic Data From Large Language Models

Synthetic data generation with Large Language Models is a promising paradigm for augmenting natural data over a nearly infinite range of tasks. Given this variety, direct comparisons among synthetic data generation algorithms are scarce, making it difficult to understand where improvement comes from and what bottlenecks exist. We propose to evaluate algorithms via the makeup of synthetic data generated by each algorithm in terms of data quality, diversity, and complexity. We choose these three characteristics for their significance in open-ended processes and the impact each has on the capabilities of downstream models. We find quality to be essential for in-distribution model generalization, diversity to be essential for out-of-distribution generalization, and complexity to be beneficial for both. Further, we emphasize the existence of Quality-Diversity trade-offs in training data and the downstream effects on model performance. We then examine the effect of various components in the synthetic data pipeline on each data characteristic. This examination allows us to taxonomize and compare synthetic data generation algorithms through the components they utilize and the resulting effects on data QDC composition. This analysis extends into a discussion on the importance of balancing QDC in synthetic data for efficient reinforcement learning and self-improvement algorithms. Analogous to the QD trade-offs in training data, often there exist trade-offs between model output quality and output diversity which impact the composition of synthetic data. We observe that many models are currently evaluated and optimized only for output quality, thereby limiting output diversity and the potential for self-improvement. We argue that balancing these trade-offs is essential to the development of future self-improvement algorithms and highlight a number of works making progress in this direction.

Towards Utilising a Range of Neural Activations for Comprehending Representational Associations

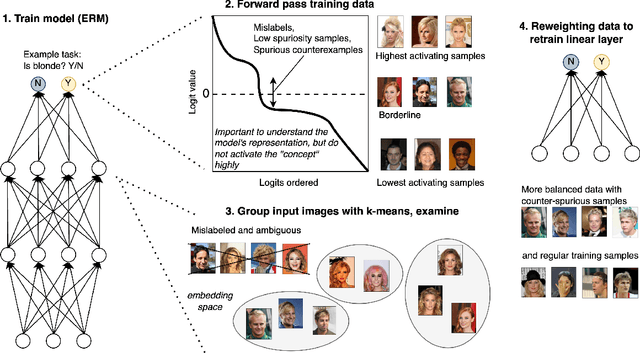
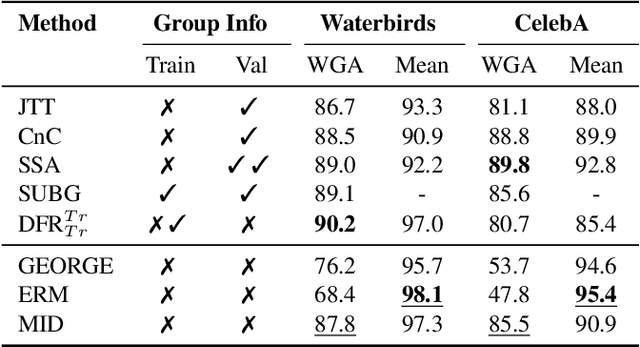
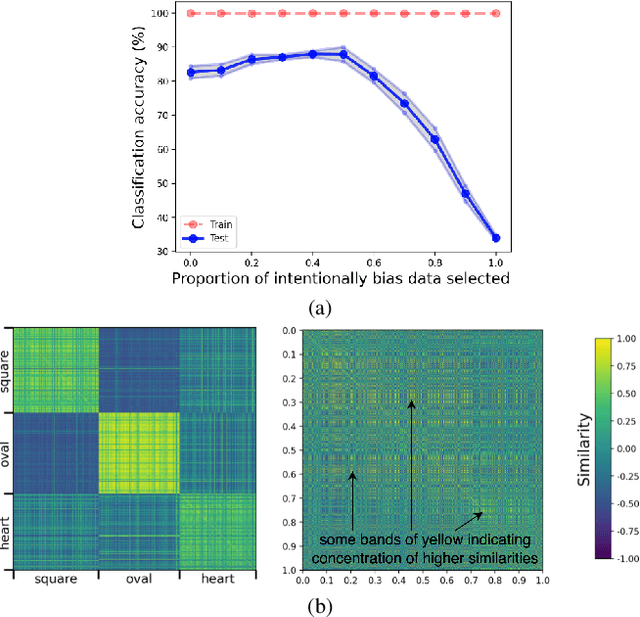
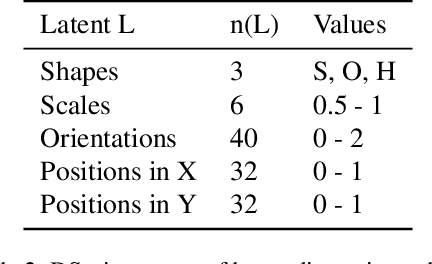
Recent efforts to understand intermediate representations in deep neural networks have commonly attempted to label individual neurons and combinations of neurons that make up linear directions in the latent space by examining extremal neuron activations and the highest direction projections. In this paper, we show that this approach, although yielding a good approximation for many purposes, fails to capture valuable information about the behaviour of a representation. Neural network activations are generally dense, and so a more complex, but realistic scenario is that linear directions encode information at various levels of stimulation. We hypothesise that non-extremal level activations contain complex information worth investigating, such as statistical associations, and thus may be used to locate confounding human interpretable concepts. We explore the value of studying a range of neuron activations by taking the case of mid-level output neuron activations and demonstrate on a synthetic dataset how they can inform us about aspects of representations in the penultimate layer not evident through analysing maximal activations alone. We use our findings to develop a method to curate data from mid-range logit samples for retraining to mitigate spurious correlations, or confounding concepts in the penultimate layer, on real benchmark datasets. The success of our method exemplifies the utility of inspecting non-maximal activations to extract complex relationships learned by models.

On the Detection of Anomalous or Out-Of-Distribution Data in Vision Models Using Statistical Techniques

Out-of-distribution data and anomalous inputs are vulnerabilities of machine learning systems today, often causing systems to make incorrect predictions. The diverse range of data on which these models are used makes detecting atypical inputs a difficult and important task. We assess a tool, Benford's law, as a method used to quantify the difference between real and corrupted inputs. We believe that in many settings, it could function as a filter for anomalous data points and for signalling out-of-distribution data. We hope to open a discussion on these applications and further areas where this technique is underexplored.

Disentangling Neuron Representations with Concept Vectors

Mechanistic interpretability aims to understand how models store representations by breaking down neural networks into interpretable units. However, the occurrence of polysemantic neurons, or neurons that respond to multiple unrelated features, makes interpreting individual neurons challenging. This has led to the search for meaningful vectors, known as concept vectors, in activation space instead of individual neurons. The main contribution of this paper is a method to disentangle polysemantic neurons into concept vectors encapsulating distinct features. Our method can search for fine-grained concepts according to the user's desired level of concept separation. The analysis shows that polysemantic neurons can be disentangled into directions consisting of linear combinations of neurons. Our evaluations show that the concept vectors found encode coherent, human-understandable features.